Prove that the diameter is the greatest chord in a circle.
Step by step video & image solution for Prove that the diameter is the greatest chord in a circle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
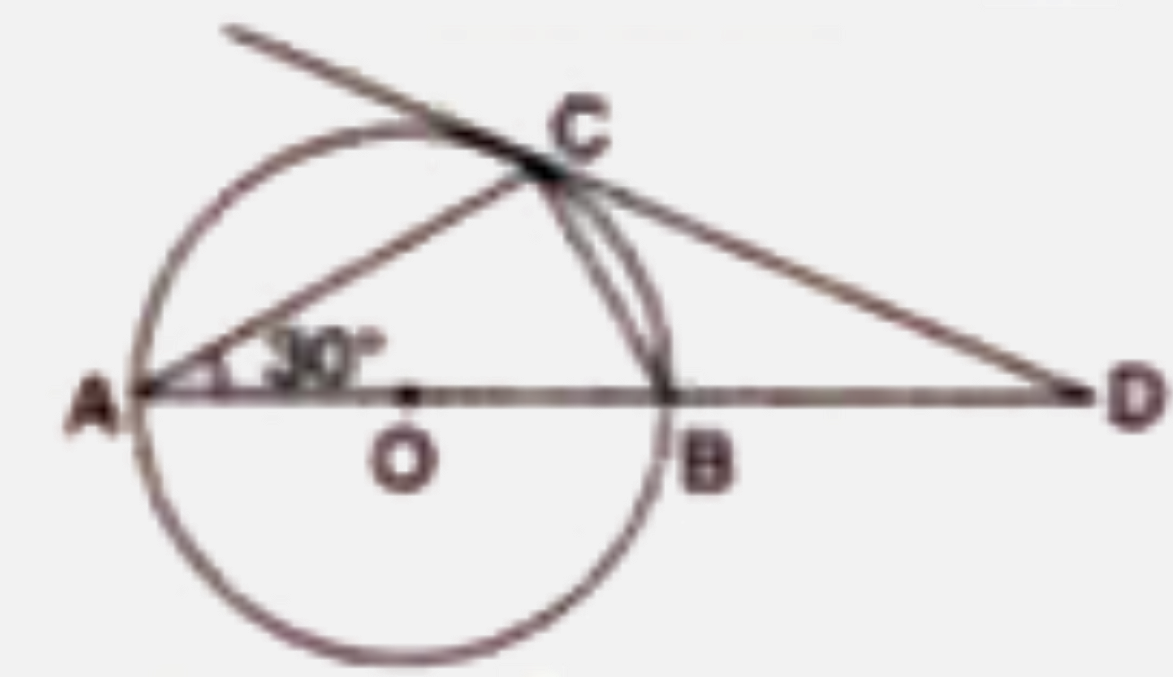
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the circle described on the focal chord of parabola as a diameter touches the directrix
View SolutionFill in the blanks: (i) The diameter of a circle is … times its radius (ii) The diameter of a circle is the … chord of the circle. (iii) The diameter of a circle pass through…. (iv) A chord of a circle is a line segment with its end points on the … (v) If we join any two points on a circle by a line segment, we obtain… (vi) A radius of a circle is a line segment with one end at …. and the other end at…. (vii) All radii of a circle are… (viii) The diameters of circle are… (ix) The total number of diameters of circle is… (x) Every point on a circle is…from its centre.. (xi) A chord of a circle contains exactly….points of the circle.. (xii) A diameter is the longest… (xiii) Concentric circles are circle having….
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionIf PandQ a be a pair of conjugate points with respect to a circle S. Prove that the circle on PQ as diameter cuts the circle S orthogonally.
View Solution
