A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12cm.
To solve the problem of finding the surface area of the toy shaped like a right circular cylinder with a hemisphere on one end and a cone on the other, we will follow these steps:
Step 1: Identify the dimensions
- Radius (r) of the cylindrical part = 5 cm
- Height (h) of the cylindrical part = 13 cm
- Height (h_cone) of the conical part = 12 cm
- The radius of the hemisphere is the same as that of the cylinder, which is also 5 cm.
Step 2: Calculate the surface area of the hemisphere
The formula for the surface area of a hemisphere (excluding the base) is given by:
Surface Area of Hemisphere=2πr2
Substituting the value of r:
Surface Area of Hemisphere=2π(5)2=2π(25)=50πcm2
Step 3: Calculate the surface area of the cylinder
The formula for the curved surface area of a cylinder is:
Surface Area of Cylinder=2πrh
Substituting the values of r and h:
Surface Area of Cylinder=2π(5)(13)=130πcm2
Step 4: Calculate the slant height of the cone
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√h2cone+r2
Substituting the values:
l=√(12)2+(5)2=√144+25=√169=13cm
Step 5: Calculate the surface area of the cone
The formula for the curved surface area of a cone is:
Surface Area of Cone=πrl
Substituting the values of r and l:
Surface Area of Cone=π(5)(13)=65πcm2
Step 6: Calculate the total surface area of the toy
The total surface area of the toy is the sum of the surface areas of the hemisphere, cylinder, and cone:
Total Surface Area=Surface Area of Hemisphere+Surface Area of Cylinder+Surface Area of Cone
Substituting the calculated values:
Total Surface Area=50π+130π+65π=245πcm2
Using the approximation π≈3.14:
Total Surface Area≈245×3.14≈769.3cm2
Rounding it off, we can say:
Total Surface Area≈770cm2
Final Answer:
The total surface area of the toy is approximately 770 cm².
---
- Radius (r) of the cylindrical part = 5 cm
- Height (h) of the cylindrical part = 13 cm
- Height (h_cone) of the conical part = 12 cm
- The radius of the hemisphere is the same as that of the cylinder, which is also 5 cm.
The formula for the surface area of a hemisphere (excluding the base) is given by:
Surface Area of Hemisphere=2πr2
Substituting the value of r:
Surface Area of Hemisphere=2π(5)2=2π(25)=50πcm2
The formula for the curved surface area of a cylinder is:
Surface Area of Cylinder=2πrh
Substituting the values of r and h:
Surface Area of Cylinder=2π(5)(13)=130πcm2
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√h2cone+r2
Substituting the values:
l=√(12)2+(5)2=√144+25=√169=13cm
The formula for the curved surface area of a cone is:
Surface Area of Cone=πrl
Substituting the values of r and l:
Surface Area of Cone=π(5)(13)=65πcm2
The total surface area of the toy is the sum of the surface areas of the hemisphere, cylinder, and cone:
Total Surface Area=Surface Area of Hemisphere+Surface Area of Cylinder+Surface Area of Cone
Substituting the calculated values:
Total Surface Area=50π+130π+65π=245πcm2
Using the approximation π≈3.14:
Total Surface Area≈245×3.14≈769.3cm2
Rounding it off, we can say:
Total Surface Area≈770cm2
The total surface area of the toy is approximately 770 cm².
Topper's Solved these Questions
- SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER CONEBOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDER CONEEXERCISE - All Questions
129 Videos
- TABULAR REPRESENTATION OF STATISTICAL DATA BOOK - RD SHARMA ENGLISHCHAPTER - TABULAR REPRESENTATION OF STATISTICAL DATA EXERCISE - All Questions
70 Videos
Similar Questions
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical par are 13cm and 5cm respectively. The radii of the hemispherical and conical parts re the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
View SolutionA solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and the height of the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the volume of the solid toy. (Use π=22/7 )
View SolutionA solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π=22/7 )
View SolutionFind the total surface area of a right circular cone with radius 6cm and height 8cm.
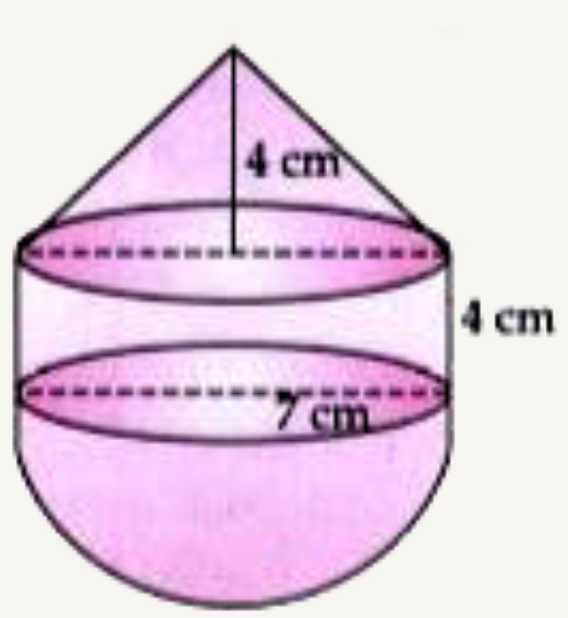
View SolutionThe following figure represents a solid consiting of right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.
View SolutionA tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also find the rate of the canvas with 500 per m2
View SolutionA tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also find the rate of the canvas with 500 per m2
View SolutionA circus tent is in the form of a right circular cylinder and right circular cone above it . The diameter and the height of the cylindrical part of the tent are 126 m and 5 m respectively.The totla height of the tent is 21 m. Find the total cost of the tent if the canvas used costsRs 12 per square metre.
View SolutionA rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diamter and height of the cylinder are 6 cm and 12 cm , respectively. If the slant height of the conical portion is 5 cm, the find the total surface area and volume of the rocket. ( use π=3.14).
View SolutionThe radius of the base and the height of a right circular cone are 7 cm and 24 cm respectively. Find the volume and the total surface area of the cone.
View Solution
