A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π=22/7 )
To find the total surface area of the solid which consists of a right circular cylinder, a hemisphere, and a cone, we will follow these steps:
Step 1: Identify the dimensions
- The radius r of the common base is given as 3.5cm.
- The height of the cylindrical portion h1 is 10cm.
- The height of the conical portion h2 is 6cm.
Step 2: Calculate the slant height of the cone
To find the slant height l of the cone, we use the Pythagorean theorem:
l=√r2+h22
Substituting the values:
l=√(3.5)2+(6)2=√12.25+36=√48.25≈6.95cm
Step 3: Calculate the curved surface area of the cone
The formula for the curved surface area (CSA) of a cone is:
CSAcone=πrl
Substituting the values:
CSAcone=227×3.5×6.95
Step 4: Calculate the curved surface area of the cylinder
The formula for the curved surface area of a cylinder is:
CSAcylinder=2πrh1
Substituting the values:
CSAcylinder=2×227×3.5×10
Step 5: Calculate the curved surface area of the hemisphere
The formula for the curved surface area of a hemisphere is:
CSAhemisphere=2πr2
Substituting the values:
CSAhemisphere=2×227×(3.5)2
Step 6: Calculate the total surface area
The total surface area (TSA) of the solid is the sum of the curved surface areas of the cone, cylinder, and hemisphere:
TSA=CSAcone+CSAcylinder+CSAhemisphere
Step 7: Substitute and calculate
1. Calculate each of the curved surface areas:
- For the cone:
CSAcone=227×3.5×6.95≈22×0.5×6.95≈11×6.95≈76.45cm2
- For the cylinder:
CSAcylinder=2×227×3.5×10≈2×22×0.5×10=220cm2
- For the hemisphere:
CSAhemisphere=2×227×(3.5)2≈2×227×12.25≈2×22×1.75≈77cm2
2. Add them together:
TSA=76.45+220+77≈373.45cm2
Final Answer
Therefore, the total surface area of the solid is:
Total Surface Area=373.45cm2
- The radius r of the common base is given as 3.5cm.
- The height of the cylindrical portion h1 is 10cm.
- The height of the conical portion h2 is 6cm.
To find the slant height l of the cone, we use the Pythagorean theorem:
l=√r2+h22
Substituting the values:
l=√(3.5)2+(6)2=√12.25+36=√48.25≈6.95cm
The formula for the curved surface area (CSA) of a cone is:
CSAcone=πrl
Substituting the values:
CSAcone=227×3.5×6.95
The formula for the curved surface area of a cylinder is:
CSAcylinder=2πrh1
Substituting the values:
CSAcylinder=2×227×3.5×10
The formula for the curved surface area of a hemisphere is:
CSAhemisphere=2πr2
Substituting the values:
CSAhemisphere=2×227×(3.5)2
The total surface area (TSA) of the solid is the sum of the curved surface areas of the cone, cylinder, and hemisphere:
TSA=CSAcone+CSAcylinder+CSAhemisphere
1. Calculate each of the curved surface areas:
- For the cone:
CSAcone=227×3.5×6.95≈22×0.5×6.95≈11×6.95≈76.45cm2
- For the cylinder:
CSAcylinder=2×227×3.5×10≈2×22×0.5×10=220cm2
- For the hemisphere:
CSAhemisphere=2×227×(3.5)2≈2×227×12.25≈2×22×1.75≈77cm2
TSA=76.45+220+77≈373.45cm2
Therefore, the total surface area of the solid is:
Total Surface Area=373.45cm2
Topper's Solved these Questions
Similar Questions
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm. and the height of the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the volume of the solid toy. (Use π=22/7 )
View SolutionThe radius of the base and the height of a right circular cone are 7 cm and 24 cm respectively. Find the volume and the total surface area of the cone.
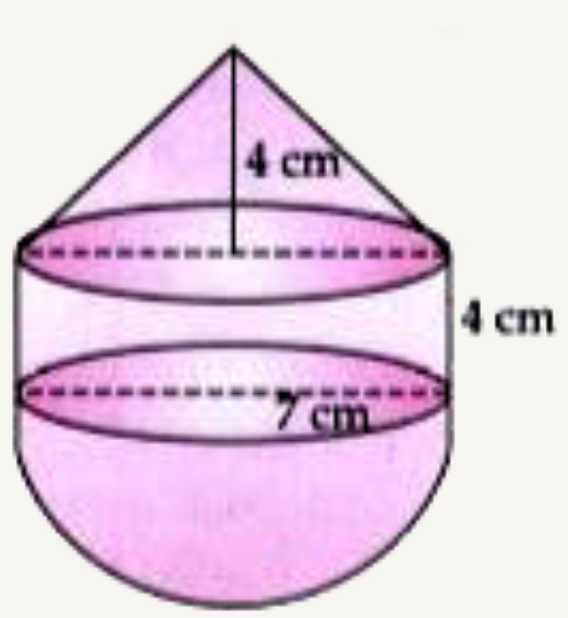
View SolutionThe following figure represents a solid consiting of right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12cm.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical par are 13cm and 5cm respectively. The radii of the hemispherical and conical parts re the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
View SolutionA toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if height of the conical part is 12cm.
View SolutionIf the radii of the circular ends of a conical bucket of height 16 cm are 20 cm and 8 cm, find the capacity and total surface area of the bucket. [Use pi= 22/7]
View Solution. If the radii of the circular ends of a conical bucket, which is 16 cm high, are 20 cm and 8 cm, find the capacity and total surface area of the bucket. [Use pi= 22/7]
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View Solution
