Question

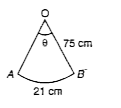
Find the angle in radian
through which a pendulum swings if its length is 75 cm and the tip describes
an arc of length
(i) 10 cm    (ii) 15 cm   (iii)
21 cm

Explanation

To find the angle in radians through which a pendulum swings, we can use the formula:

$$\theta =\frac{l}{r}$$

where:
- $$\theta$$ is the angle in radians,
- $$l$$ is the length of the arc,
- $$r$$ is the radius (length of the pendulum).

Given that the length of the pendulum (radius) is $$r=75$$ cm, we will calculate $$\theta$$ for each arc length provided.

Part (i): Arc Length $$l=10$$ cm

1. Substitute the values into the formula:
\( \theta = \frac{l}{r} = \frac{10}{75} \)

2. Simplify the fraction:
\( \theta = \frac{10 \div 5}{75 \div 5} = \frac{2}{15} \)

Thus, the angle for the first part is:
\( \theta = \frac{2}{15} \text{ radians} \)

Part (ii): Arc Length \(l = 15\) cm

1. Substitute the values into the formula:
\( \theta = \frac{l}{r} = \frac{15}{75} \)

2. Simplify the fraction:
\( \theta = \frac{15 \div 15}{75 \div 15} = \frac{1}{5} \)

Thus, the angle for the second part is:
\( \theta = \frac{1}{5} \text{ radians} \)

Part (iii): Arc Length \(l = 21\) cm

1. Substitute the values into the formula:
\( \theta = \frac{l}{r} = \frac{21}{75} \)

2. Simplify the fraction:
\( \theta = \frac{21 \div 3}{75 \div 3} = \frac{7}{25} \)

Thus, the angle for the third part is:
\( \theta = \frac{7}{25} \text{ radians} \)

Summary of Results:
- For \(l = 10\) cm, \(\theta = \frac{2}{15}\) radians
- For \(l = 15\) cm, \(\theta = \frac{1}{5}\) radians
- For \(l = 21\) cm, \(\theta = \frac{7}{25}\) radians