A railway train is travelling on a circular curve of 1500 metres radius at the rate of 66km/hr. Through what angle has it turned in 10 seconds?
To solve the problem step by step, we will follow the process outlined in the video transcript.
Step 1: Convert the speed from km/hr to m/s
The speed of the train is given as 66 km/hr. We need to convert this speed into meters per second (m/s).
Conversion Formula:
Speed in m/s=Speed in km/hr×518
Calculation:
Speed=66×518=33018=553 m/s
Step 2: Calculate the distance covered in 10 seconds
Now that we have the speed in m/s, we can calculate the distance covered by the train in 10 seconds.
Formula:
Distance=Speed×Time
Calculation:
Distance=553 m/s×10 s=5503 meters
Step 3: Use the formula to find the angle turned
We know that the arc length (l) is related to the radius (r) and the angle (θ) in radians by the formula:
l=rθ
Rearranging this formula gives us:
θ=lr
Step 4: Substitute the values into the formula
We have:
- Arc length l=5503 meters
- Radius r=1500 meters
Calculation:
θ=55031500=5503×1500=5504500=1190 radians
Final Answer
The angle turned by the train in 10 seconds is 1190 radians.
---
The speed of the train is given as 66 km/hr. We need to convert this speed into meters per second (m/s).
Speed in m/s=Speed in km/hr×518
Speed=66×518=33018=553 m/s
Now that we have the speed in m/s, we can calculate the distance covered by the train in 10 seconds.
Distance=Speed×Time
Distance=553 m/s×10 s=5503 meters
We know that the arc length (l) is related to the radius (r) and the angle (θ) in radians by the formula:
l=rθ
Rearranging this formula gives us:
θ=lr
We have:
- Arc length l=5503 meters
- Radius r=1500 meters
θ=55031500=5503×1500=5504500=1190 radians
The angle turned by the train in 10 seconds is 1190 radians.
Topper's Solved these Questions
Similar Questions
A railway train is travelling on a curve of 750 m radius at the rate of 30 km/h, through what angle has it turned in 10 seconds ?
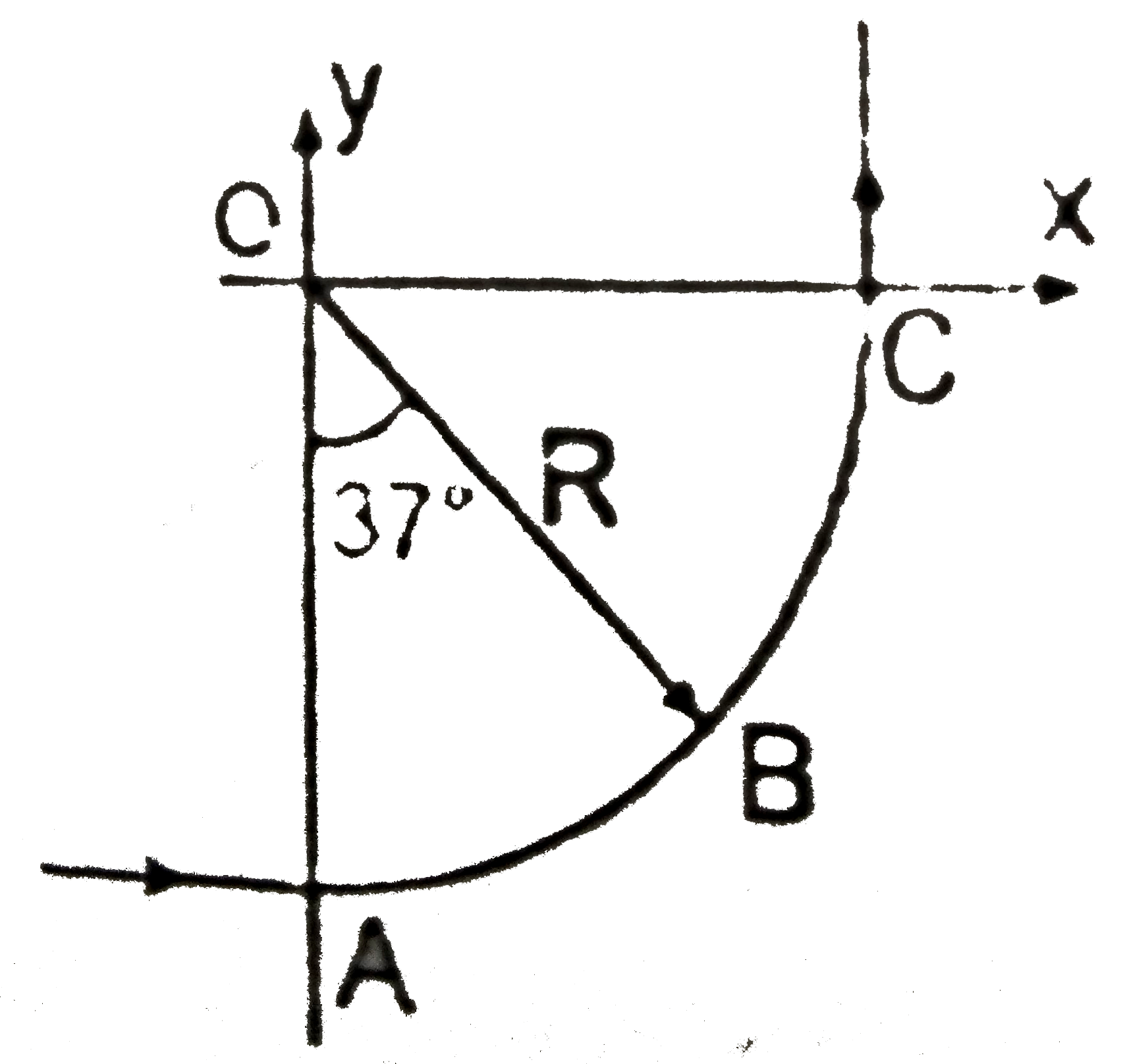
View SolutionA car initially travelling eastwards turns noth by travelling in a quarter circular path of radius R metres at uniform speed as shown in figure. The car completes the turn in T second.
(a) What is the acceleration of the car when it is at B located at an angle of 37∘. Express your a swers in terms of unit vectors ˆi and ˆj.
(b) The magnitude of car's average acceleration during T second period.
View SolutionA wheel starts from rest and attains an angular velocity of 20 radian/s after being uniformly accelerated for 10 s. The total angle in radian through which it has turned in 10 second is
View SolutionA particle is travelling in a circular path of radius 4m. At a certain instant the particle is moving at 20m/s and its acceleration is at an angle of 37∘ from the direction to the centre of the circle as seen from the particle
(i) At what rate is the speed of the particle increasing?
(ii) What is the magnitude of the acceleration?
View SolutionA racing car travelling at 35ms−1 along a circular path of radius 700 m, starts picking up speed at the rate of 2ms−2 What is its total acceleration ?
View SolutionA motor car travelling at 30m/s on a circular road of radius 500m. It is increasing its speed at the rate of 2ms−2. What its accleration at that instant ?
View SolutionA car is travelling along a circular curve that has a radius of 50m . If its speed is 16m/s and is increasing uniformly at 8m/s2 . Determine the magnitude of its acceleration at this instant.
View SolutionAn aeroplane travelling at a speed of 500 km/hr tilts at an angle of 30° as it makes a turn. What is the radius of the curve ?
View SolutionThe shaft of a motor rotates at a constant speed of 1800 rpm. What is the angle in radians it has turned through in one second ?
View SolutionA car is travelling with linear velocity v on a circular road of radius r. If it is increasing its speed at the rate of a metre/sec2, then the resultant acceleration will be
View Solution
