Question

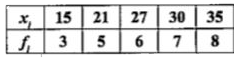
Find the mean deviation from the median of the following data:








15


21


27


30









3


5


6


7



 

Explanation

To find the mean deviation from the median of the given data, we will follow these steps:

Step 1: Organize the Data
We have the following data points and their corresponding frequencies:

| \(x_i\) | Frequency (\(f_i\)) |
|---------|---------------------|
| 15 | 3 |
| 21 | 5 |
| 27 | 6 |
| 30 | 7 |

Step 2: Calculate Cumulative Frequency
Next, we calculate the cumulative frequency (\(CF\)):

| \(x_i\) | Frequency (\(f_i\)) | Cumulative Frequency (\(CF\)) |
|---------|---------------------|-------------------------------|
| 15 | 3 | 3 |
| 21 | 5 | 8 |
| 27 | 6 | 14 |
| 30 | 7 | 21 |

Step 3: Find the Median
To find the median, we calculate \(N/2\), where \(N\) is the total frequency:

\( N = 3 + 5 + 6 + 7 = 21 \)
\( N/2 = 21/2 = 10.5 \)

Now, we look for the cumulative frequency that is just greater than 10.5. The cumulative frequency of 14 (for \(x_i = 27\)) is the first value greater than 10.5. Thus, the median is:

\( \text{Median} = 27 \)

Step 4: Calculate \(|x_i - \text{Median}|\)
Now, we calculate the absolute deviations from the median:

| \(x_i\) | \(|x_i - \text{Median}|\) | Frequency (\(f_i\)) | \(f_i \times |x_i - \text{Median}|\) |
|---------|---------------------------|---------------------|------------------------------------|
| 15 | \(|15 - 27| = 12\) | 3 | \(3 \times 12 = 36\) |
| 21 | \(|21 - 27| = 6\) | 5 | \(5 \times 6 = 30\) |
| 27 | \(|27 - 27| = 0\) | 6 | \(6 \times 0 = 0\) |
| 30 | \(|30 - 27| = 3\) | 7 | \(7 \times 3 = 21\) |

Step 5: Sum of \(f_i \times |x_i - \text{Median}|\)
Now we sum the values from the last column:

\( \text{Sum} = 36 + 30 + 0 + 21 = 87 \)

Step 6: Calculate Mean Deviation
Finally, we use the formula for mean deviation:

\( \text{Mean Deviation} = \frac{1}{N} \sum (f_i \times |x_i - \text{Median}|) \)
\( \text{Mean Deviation} = \frac{1}{21} \times 87 = \frac{87}{21} \approx 4.14 \)

Final Answer
The mean deviation from the median is approximately 4.14.

---