A salesman has the following record of sales during three months for three items A,BandC which have different rates of commission Month, Sale of units, Total commissiondrawn (in Rs) Find out the rates of commission on items A,BandC by using deter-minant method.
To solve the problem of finding the rates of commission on items A, B, and C using the determinant method, we will follow these steps:
Step 1: Set Up the Problem
Let's denote the rates of commission for items A, B, and C as x, y, and z respectively. We will create a system of equations based on the sales data provided for three months.
Step 2: Formulate the Equations
Assuming we have the following sales data for three months:
- Month 1:
- Units Sold: a1 for A, b1 for B, c1 for C
- Total Commission: C1
- Month 2:
- Units Sold: a2 for A, b2 for B, c2 for C
- Total Commission: C2
- Month 3:
- Units Sold: a3 for A, b3 for B, c3 for C
- Total Commission: C3
From this data, we can form the following equations:
1. a1x+b1y+c1z=C1
2. a2x+b2y+c2z=C2
3. a3x+b3y+c3z=C3
Step 3: Write the Coefficient Matrix and the Constant Matrix
The coefficient matrix A and the constant matrix B can be represented as follows:
A=⎡⎢⎣a1b1c1a2b2c2a3b3c3⎤⎥⎦,B=⎡⎢⎣C1C2C3⎤⎥⎦
Step 4: Calculate the Determinant of Matrix A
To find the rates of commission x,y,z, we first need to calculate the determinant of matrix A:
det(A)=a1(b2c3−b3c2)−b1(a2c3−a3c2)+c1(a2b3−a3b2)
Step 5: Calculate the Determinants for x,y,z
Next, we will find the determinants for x,y,z by replacing the respective columns of A with B:
1. For x:
det(Ax)=∣∣
∣∣C1b1c1C2b2c2C3b3c3∣∣
∣∣
2. For y:
det(Ay)=∣∣
∣∣a1C1c1a2C2c2a3C3c3∣∣
∣∣
3. For z:
det(Az)=∣∣
∣∣a1b1C1a2b2C2a3b3C3∣∣
∣∣
Step 6: Solve for x,y,z
Using Cramer's Rule, we can find the values of x,y,z as follows:
x=det(Ax)det(A),y=det(Ay)det(A),z=det(Az)det(A)
Step 7: Conclusion
After calculating the determinants and substituting them into the equations, we will have the rates of commission for items A, B, and C.
Let's denote the rates of commission for items A, B, and C as x, y, and z respectively. We will create a system of equations based on the sales data provided for three months.
Assuming we have the following sales data for three months:
- Units Sold: a1 for A, b1 for B, c1 for C
- Total Commission: C1
- Units Sold: a2 for A, b2 for B, c2 for C
- Total Commission: C2
- Units Sold: a3 for A, b3 for B, c3 for C
- Total Commission: C3
1. a1x+b1y+c1z=C1
2. a2x+b2y+c2z=C2
3. a3x+b3y+c3z=C3
The coefficient matrix A and the constant matrix B can be represented as follows:
To find the rates of commission x,y,z, we first need to calculate the determinant of matrix A:
Next, we will find the determinants for x,y,z by replacing the respective columns of A with B:
det(Ax)=∣∣
∣∣C1b1c1C2b2c2C3b3c3∣∣
∣∣
det(Ay)=∣∣
∣∣a1C1c1a2C2c2a3C3c3∣∣
∣∣
det(Az)=∣∣
∣∣a1b1C1a2b2C2a3b3C3∣∣
∣∣
Using Cramer's Rule, we can find the values of x,y,z as follows:
After calculating the determinants and substituting them into the equations, we will have the rates of commission for items A, B, and C.
Topper's Solved these Questions
Similar Questions
The given bar graph shows the number of identical articles sold by 5 different stores A, B, C, D and E during a particular month.

Study the bar graph and answer the following questions :
(i) Which store sold the largest number of articles ?
(ii) By what per cent is the sale of store D more than that of store B ?
(iii) Find the ratio of the total sale of the two highest selling stores to the total sale of the two least selling stores.
(iv) By how much must store E increase its sale to catch up with its nearest rival store ?
View SolutionThe prices of three commodities P, Q, and R are Rs x, y and z per unit respectively. A purchases 4 units of R and sells 3 unit of P and 5 units of Q. B purchases 3 units of Q and sells 2 units of P and 1 unit of R. C purchases 1 unit of P and sells 4 units of Q and 6 units of R. In the process A, B and C earn Rs 6000, 5000 and 13000 respectively. If selling the units is positive earning and buying the units is negative earnings, find the price per unit of three commodities by using matrix method.
View Solution
Knowledge Check
he flu shot for a flu seaons is created four strains of the flu virus, named Strain A,B,C and D, respectively. Medical researchers use the following data to determine the effectiveness of the vacine over the flu season. Table 1 shows the effectiveness of the vaccine against each of these strains individually. The graph below the table shows the prevalence of each of these strains during each month of the flu season, represented as a percentage of the overall cases of flu that month.
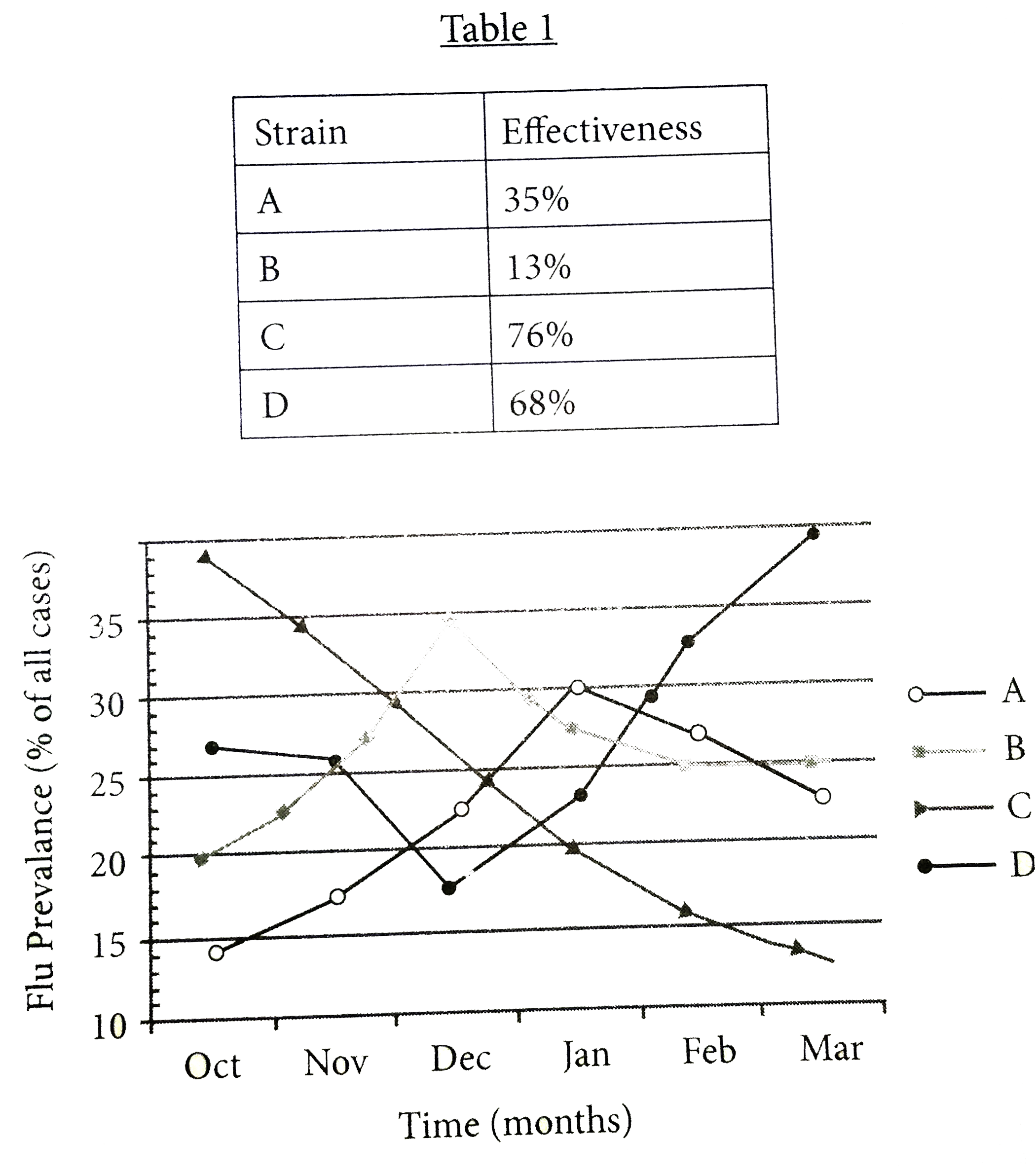
For the strain against which the flu shot was the most effective. approximately how effective was the shot overall during the month that strain was least prevalent?A0.13B0.2C0.27D0.48The figure below depicts life-histroy strategies for three plant species (a,b and c) along 3 axes : strength of competition with other organisms, level of distrubance in the habitat, and level of environmental stress in the habitat. Species a grows in habitats where competition among species b grown in habitats with and stress are low. Species b grows in habitats with high environmental stress but with low interspecies competition. Species c grows in highly disturbed habitats with low enviornmental stress.
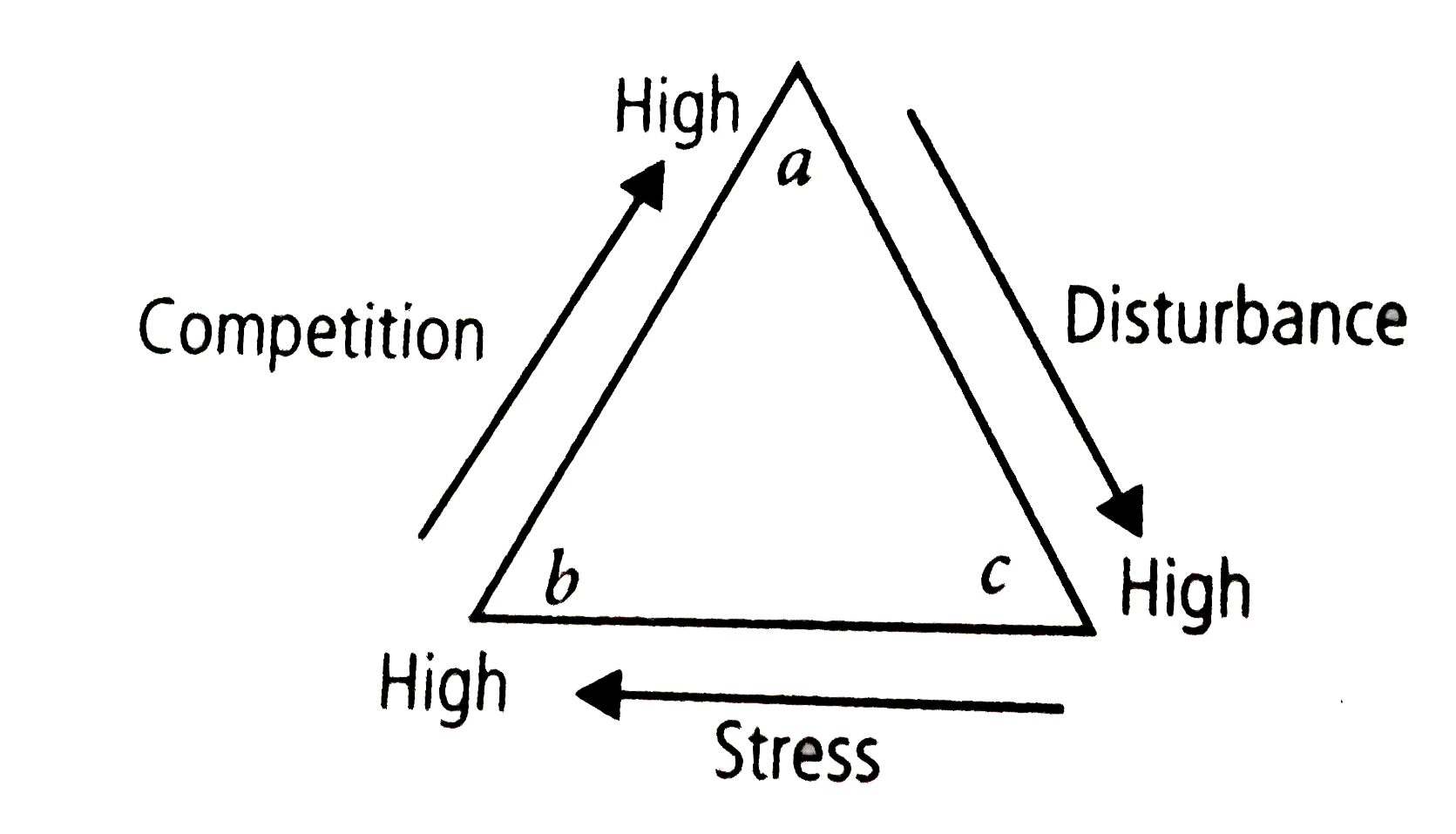 Which of the statements below is/are correct ?
Which of the statements below is/are correct ?
I. Characteristics of "a-type" plants are faster growth rate and short-lived leaves.
II. Desert annual plants are "b-type" species. they have rapid growth and produce large amount of seeds in a short time after rains.
III. Most plants belonging to "c-type" species would be herbaceous while "a-type" and "b-types" species are likely to be trees or shrubs.AOnly IIBI and IICI and IIIDII and III
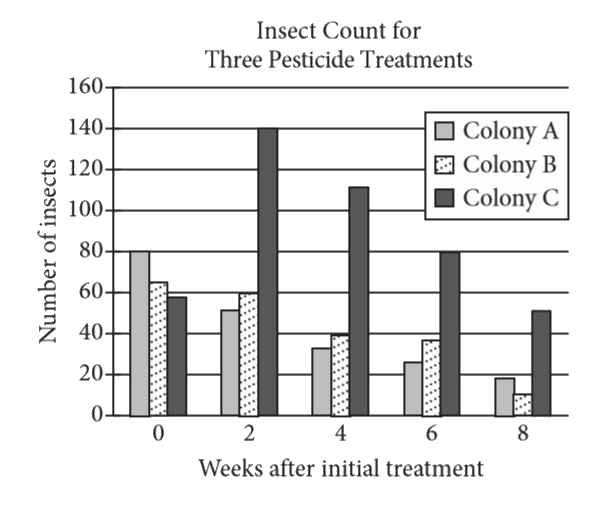
Three colonies of insects were each treated with a different pesticide over an 8-week period to test the effectiveness of the three pesticides. Colonies A, B, and C were treated with Pesticides A, B, and C, respectively. Each pesticide was applied every 2 weeks to one of the three colonies over the 8-week period. The bar graph above shows the insect counts for each of the three colonies 0, 2, 4, 6, and 8 weeks after the initial treatment.
Of the following, which is closest to the ratio of the total number of insects in all three colonies in week 8 to the total number of insects at the time of initial treatment?
View SolutionA rubber company is engaged in producing three types of tyres A, B and C. each type requires processing in two plants, Plant I and Plant II. The capacities of the two plants, in number of tyres per day, are as follows: Plants A B C I 50 100 100 II 60 60 200 The monthly demand for tyre A, B and C is 2500, 3000 and 7000 respectively. If plant I costs Rs. 2500 per day, and plant II costs R. 2500 per day to operate , how many days should each be run per month to minimize cost while meeting the demand? Formulate the problem as LPP.
View SolutionKrishna has an apple orchard which has a 10m×10m sized kitchen garden attached to it. she divides it into a 10×10 grid and puts soil and manure into it. she grows a lemon plant at A, a coriander plant at B, an onion plant at C and a tomato plant at D. Her husband Ram praised her kitchen garden and points out that on joining A,B,C and D they may form a parallelogram. look at the below figure carefully and answer the following questions: (i) write the coordinates of the points A,B,C and D using the 10×10 grid as coordinate axes. (ii) find whether ABCD is a parallelogram or not.
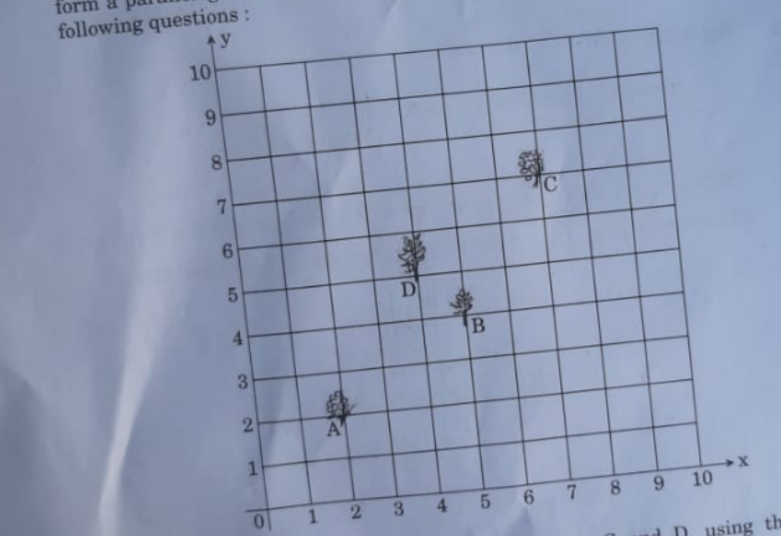
View Solutionkrishna has an apple orchard which has a 10m×10m sized kitchen garden attached to it . She divides it into a 10×10 grid and puts soil and manure into it She growns a lemon plants at . A a coriander plants at B , an onion plants at C and a tamato plants at D. Her bushand Ram prasied her kitchen graden and points out that on joining A, B, C, and D they may form a paralleleogram Look at the below. figure carefully and answer the following question.

(i) Write the coordinates of the points A,B, C and D using the 10×10 grid as coordinate axes.
(ii) Find whether ABCD is a paralleogram or not .
View SolutionThe reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
Let the equilibrium constant of Step I be 2×10−3mol−1L and the rate constants for the formation of A2X and A2 in Step II and III are 3.0×10−2mol−1L−1min and 1×103mol−1L−1min (all data at 25∘C), then what is the overall rate constant (mol−2L2−1min) of the consumption of B2?
View SolutionThe reaction 2AX(g)+2B2(g)→A2(g)+2B2X(g) has been studied kinetically and on the baiss of the rate law following mechanism has been proposed.
I. 2AX⇔A2X2 (fast and reverse)
II. A2X2+B2→A2X+B2X
III. A2X+B2→A2+B2X
where all the reaction intermediates are gases under ordinary condition.
form the above mechanism in which the steps (elementary) differ conisderably in their rates, the rate law is derived uisng the principle that the slowest step is the rate-determining step (RDS) and the rate of any step varies as the Product of the molar concentrations of each reacting speacting species raised to the power equal to their respective stoichiometric coefficients (law of mass action). If a reacting species is solid or pure liquid, its active mass, i.e., molar concentration is taken to be unity, the standard state. In qrder to find out the final rate law of the reaction, the concentration of any intermediate appearing in the rate law of the RDS is substituted in terms of the concentration of the reactant(s) by means of the law of mass action applied on equilibrium step.
How many times the rate of formation of A2 will increase if concentrations of AX is doubled and that of B2 is increased theee fold?
View Solution
