Power of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
(ln2−1)m
(ln2)2m
1m
2m
The correct Answer is:C
To solve the problem step by step, we will analyze the relationship between power, force, and displacement.
Step 1: Understand the relationship between power and force
The power P is given by the equation:
P=F⋅v
where F is the force acting on the particle and v is its velocity. From the problem, we know that:
P=v2
Thus, we can equate the two expressions for power:
F⋅v=v2
Step 2: Solve for force
From the equation F⋅v=v2, we can solve for the force F:
F=v2v=v
This indicates that the force acting on the particle is equal to its velocity.
Step 3: Apply Newton's second law
Using Newton's second law, we have:
F=m⋅a
where m is the mass of the particle and a is its acceleration. Given that the mass m=1kg, we can write:
v=m⋅a
Since m=1:
v=a
Step 4: Relate acceleration to velocity
The acceleration a can also be expressed as:
a=dvdt
Thus, we can write:
v=dvdt
Step 5: Rearranging and integrating
Rearranging gives:
dt=dvv
Now we can integrate both sides. We need to find the displacement x in terms of velocity v:
dx=v⋅dt
Substituting for dt:
dx=v⋅dvv=dv
Step 6: Set up the integral
Now we need to integrate from the initial velocity v0=1m/s to some final velocity v, and from x=0 to x:
∫x0dx=∫v1dv
This simplifies to:
x=v−1
Step 7: Express velocity in terms of time
From the earlier relationship, we have:
v=x+1
Now we need to find the relationship with time. Since we have:
dxdt=x+1
Rearranging gives:
dxx+1=dt
Step 8: Integrate with limits
Integrating both sides:
∫x0dxx+1=∫t0dt
This gives:
ln(x+1)∣∣∣x0=t∣∣∣t0
Thus:
ln(x+1)−ln(1)=t
So:
ln(x+1)=t
Step 9: Solve for displacement at t=ln2
Substituting t=ln2:
ln(x+1)=ln2
Exponentiating both sides gives:
x+1=2
Thus:
x=2−1=1m
Final Answer
The displacement of the particle in ln2 seconds is:
1m
The power P is given by the equation:
P=F⋅v
where F is the force acting on the particle and v is its velocity. From the problem, we know that:
P=v2
Thus, we can equate the two expressions for power:
F⋅v=v2
From the equation F⋅v=v2, we can solve for the force F:
F=v2v=v
This indicates that the force acting on the particle is equal to its velocity.
Using Newton's second law, we have:
F=m⋅a
where m is the mass of the particle and a is its acceleration. Given that the mass m=1kg, we can write:
v=m⋅a
Since m=1:
v=a
The acceleration a can also be expressed as:
a=dvdt
Thus, we can write:
v=dvdt
Rearranging gives:
dt=dvv
Now we can integrate both sides. We need to find the displacement x in terms of velocity v:
dx=v⋅dt
Substituting for dt:
dx=v⋅dvv=dv
Now we need to integrate from the initial velocity v0=1m/s to some final velocity v, and from x=0 to x:
∫x0dx=∫v1dv
This simplifies to:
x=v−1
From the earlier relationship, we have:
v=x+1
Now we need to find the relationship with time. Since we have:
dxdt=x+1
Rearranging gives:
dxx+1=dt
Integrating both sides:
∫x0dxx+1=∫t0dt
This gives:
ln(x+1)∣∣∣x0=t∣∣∣t0
Thus:
ln(x+1)−ln(1)=t
So:
ln(x+1)=t
Substituting t=ln2:
ln(x+1)=ln2
Exponentiating both sides gives:
x+1=2
Thus:
x=2−1=1m
The displacement of the particle in ln2 seconds is:
1m
Similar Questions
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
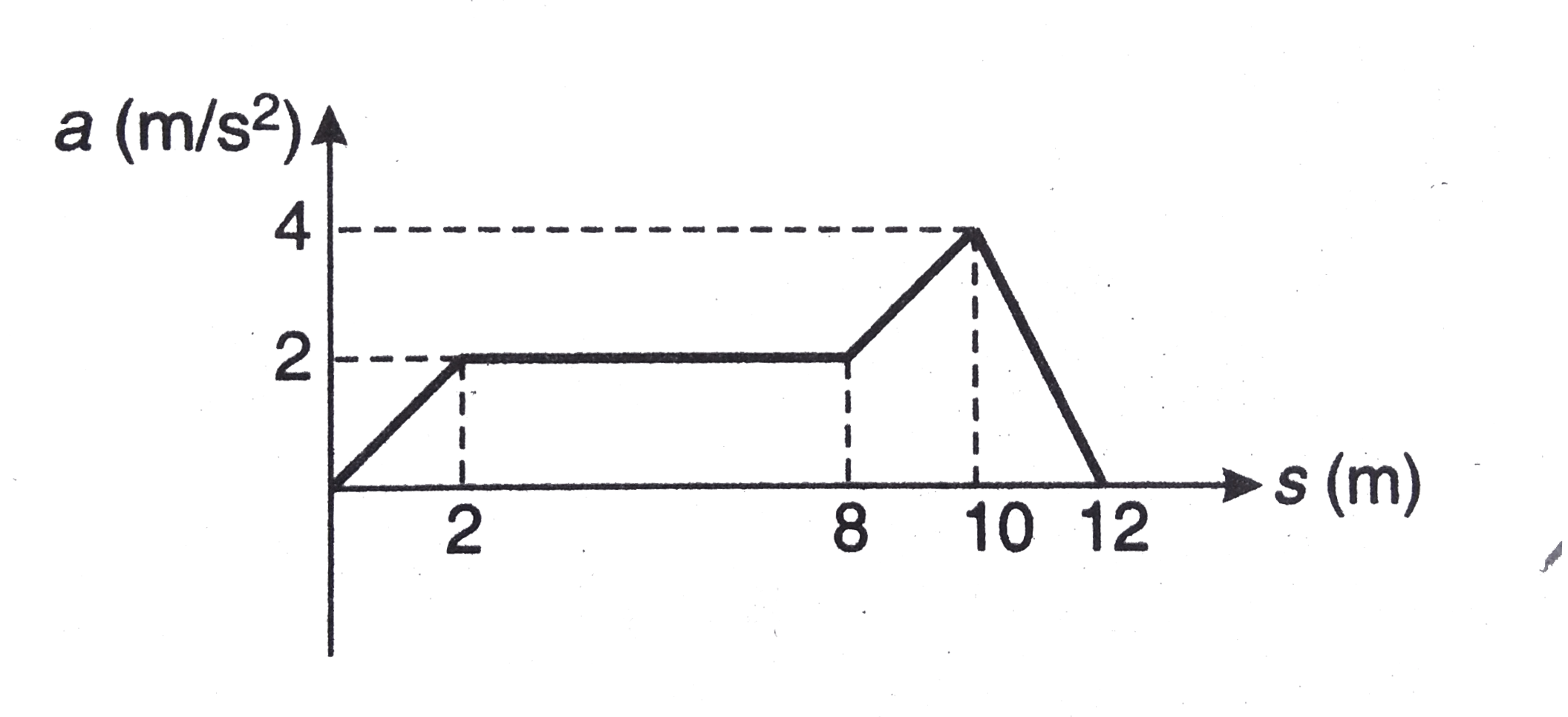
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionThe acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionA particle of mass 2kg travels along a straight line with velocity v=a√x, where a is a constant. The work done by net force during the displacement of particle from x=0 to x=4m is
View Solution