Velocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
3π[2−√32]
[2−√32]
2π[2−√32]
4π[2−√32]
The correct Answer is:A
To find the distance traveled by a particle moving along a straight line with a given velocity function V(t)=cos(π3t), we need to integrate the velocity function over the time interval from t=0 to t=2 seconds.
1. Identify the velocity function:
V(t)=cos(π3t)
2. Set up the integral for distance:
The distance x traveled by the particle from time t=0 to t=2 seconds is given by:
x=∫20V(t)dt=∫20cos(π3t)dt
3. Integrate the function:
To solve the integral, we can use the substitution method. Let:
u=π3t⇒du=π3dt⇒dt=3πdu
Changing the limits:
- When t=0, u=0
- When t=2, u=2π3
Now, we can rewrite the integral:
x=∫2π30cos(u)⋅3πdu
=3π∫2π30cos(u)du
4. Evaluate the integral:
The integral of cos(u) is sin(u):
=3π(sin(u))2π30=3π(sin(2π3)−sin(0))
=3π(sin(2π3))
Since sin(2π3)=sin(π−π3)=sin(π3)=√32:
=3π⋅√32
5. Final distance calculation:
x=3√32π
Conclusion:
The distance traveled by the particle in the first two seconds is:
x=3√32π
V(t)=cos(π3t)
The distance x traveled by the particle from time t=0 to t=2 seconds is given by:
x=∫20V(t)dt=∫20cos(π3t)dt
To solve the integral, we can use the substitution method. Let:
u=π3t⇒du=π3dt⇒dt=3πdu
Changing the limits:
- When t=0, u=0
- When t=2, u=2π3
x=∫2π30cos(u)⋅3πdu
=3π∫2π30cos(u)du
The integral of cos(u) is sin(u):
=3π(sin(u))2π30=3π(sin(2π3)−sin(0))
=3π(sin(2π3))
Since sin(2π3)=sin(π−π3)=sin(π3)=√32:
=3π⋅√32
x=3√32π
The distance traveled by the particle in the first two seconds is:
x=3√32π
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
The variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
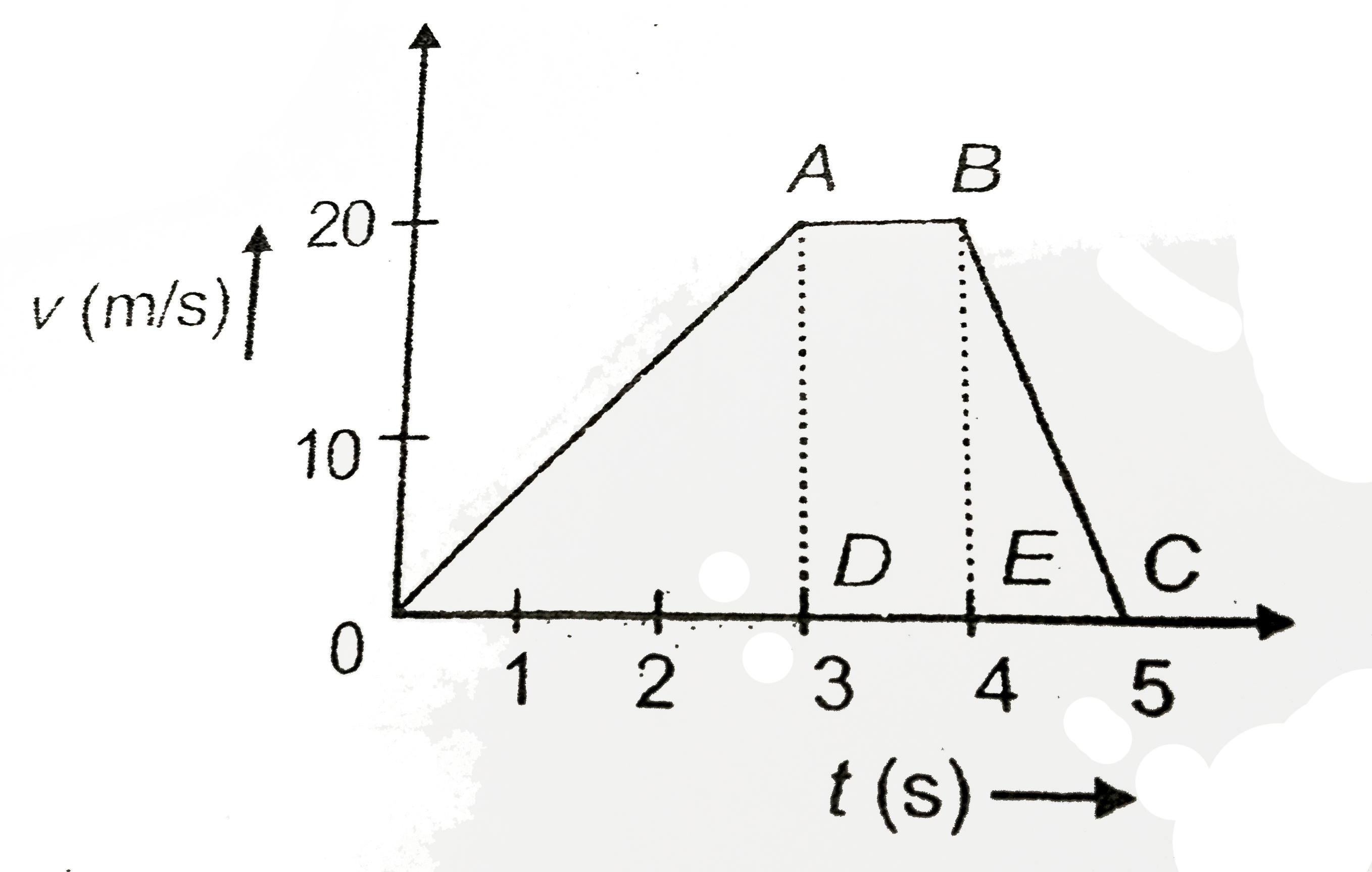
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
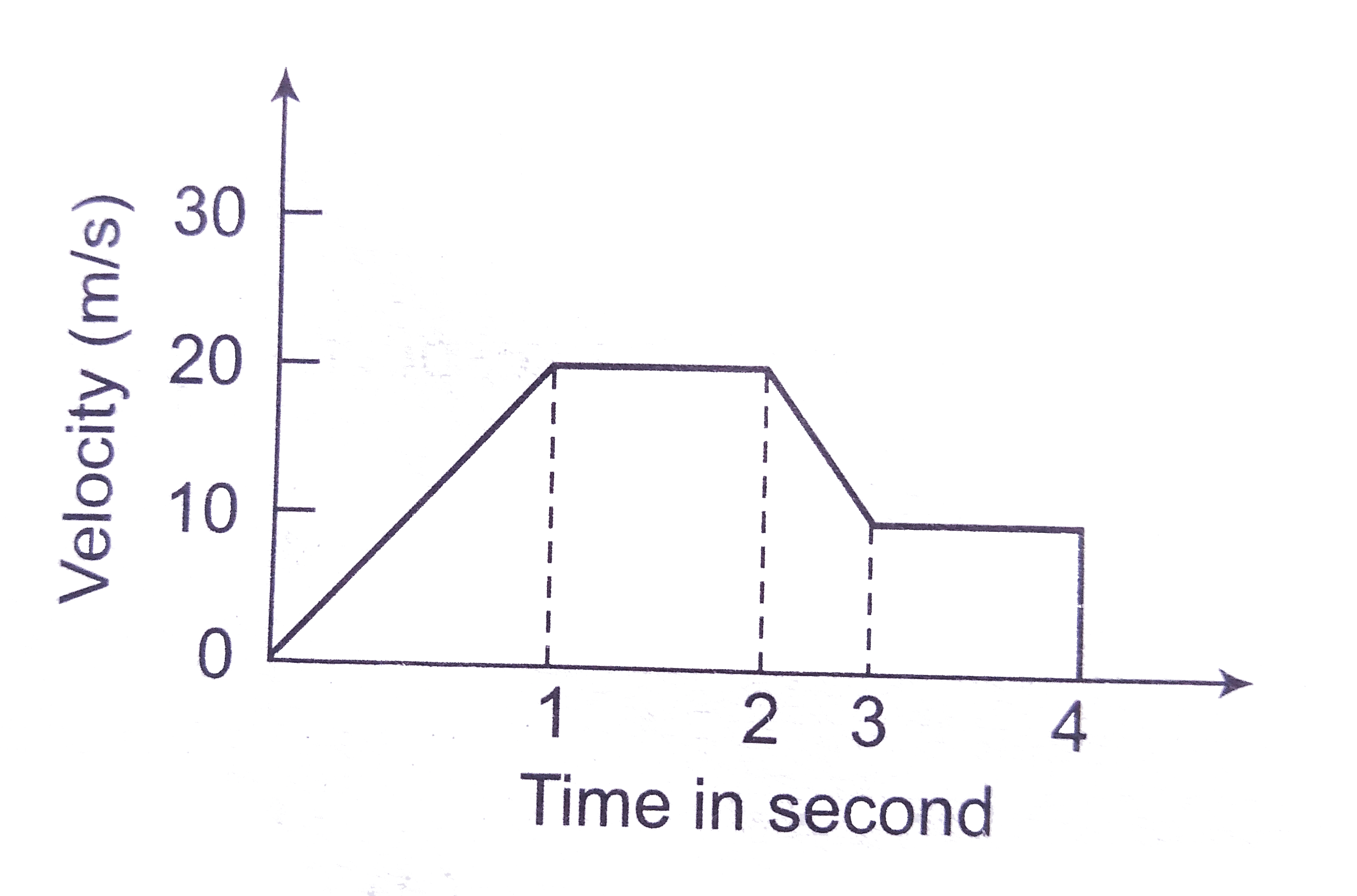
View Solution
Knowledge Check
The variataion of velocity of a particle moving along a straight line is illustrated in the following Fig. 3.1. The distance traversed by the particle in 4 seconds is
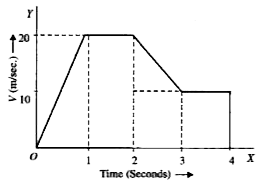 A60 mB25 mC55 mD30 m
A60 mB25 mC55 mD30 m
The position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
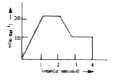
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionThe acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
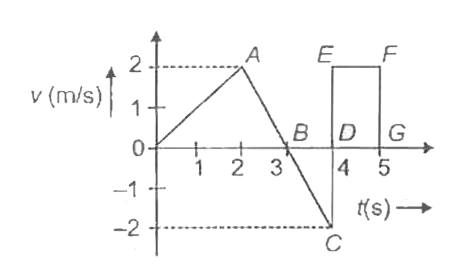
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View Solution
