A firm manufactures 3 products A, B and C. the profits are Rs. 3, 2 and 4 respectively. The firm has 2 machines and below is the required processing time in minutes for each machine on each product. Machine Products A B C M1 M2 4 2 3 2 5 4 Machines M1and M2 have 2000 and 25000 machine minutes respectively. The firm must manufacture 100 As, 200B and 50Cs but not more 150 As. Set up a LPP to maximize the profit.
To solve the problem of maximizing profit for the firm manufacturing products A, B, and C, we will set up a Linear Programming Problem (LPP).
Step 1: Define the Variables
Let:
- x = number of units of product A manufactured
- y = number of units of product B manufactured
- z = number of units of product C manufactured
Step 2: Define the Objective Function
The profit from each product is given as follows:
- Profit from product A = Rs. 3
- Profit from product B = Rs. 2
- Profit from product C = Rs. 4
Thus, the objective function to maximize profit P can be written as:
P=3x+2y+4z
Step 3: Define the Constraints
From the problem, we have the following constraints based on machine time and production requirements:
1. Machine Time Constraints:
- For Machine M1:
- The time taken for products A, B, and C is 4, 3, and 5 minutes respectively.
- The total available time for Machine M1 is 2000 minutes.
4x+3y+5z≤2000
- For Machine M2:
- The time taken for products A, B, and C is 2, 2, and 4 minutes respectively.
- The total available time for Machine M2 is 2500 minutes.
2x+2y+4z≤2500
2. Production Requirements:
- The firm must manufacture at least 100 units of A, 200 units of B, and 50 units of C:
x≥100
y≥200
z≥50
3. Upper Limit for Product A:
- The firm cannot manufacture more than 150 units of A:
x≤150
4. Non-negativity Constraints:
- The number of units produced cannot be negative:
x,y,z≥0
Step 4: Summary of the LPP
Now we can summarize the Linear Programming Problem as follows:
Maximize:
P=3x+2y+4z
Subject to:
4x+3y+5z≤2000
2x+2y+4z≤2500
x≥100
y≥200
z≥50
x≤150
x,y,z≥0
Let:
- x = number of units of product A manufactured
- y = number of units of product B manufactured
- z = number of units of product C manufactured
The profit from each product is given as follows:
- Profit from product A = Rs. 3
- Profit from product B = Rs. 2
- Profit from product C = Rs. 4
P=3x+2y+4z
From the problem, we have the following constraints based on machine time and production requirements:
- For Machine M1:
- The time taken for products A, B, and C is 4, 3, and 5 minutes respectively.
- The total available time for Machine M1 is 2000 minutes.
4x+3y+5z≤2000
- The time taken for products A, B, and C is 2, 2, and 4 minutes respectively.
- The total available time for Machine M2 is 2500 minutes.
2x+2y+4z≤2500
- The firm must manufacture at least 100 units of A, 200 units of B, and 50 units of C:
x≥100
y≥200
z≥50
- The firm cannot manufacture more than 150 units of A:
x≤150
- The number of units produced cannot be negative:
x,y,z≥0
Now we can summarize the Linear Programming Problem as follows:
P=3x+2y+4z
4x+3y+5z≤2000
2x+2y+4z≤2500
x≥100
y≥200
z≥50
x≤150
x,y,z≥0
Topper's Solved these Questions
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
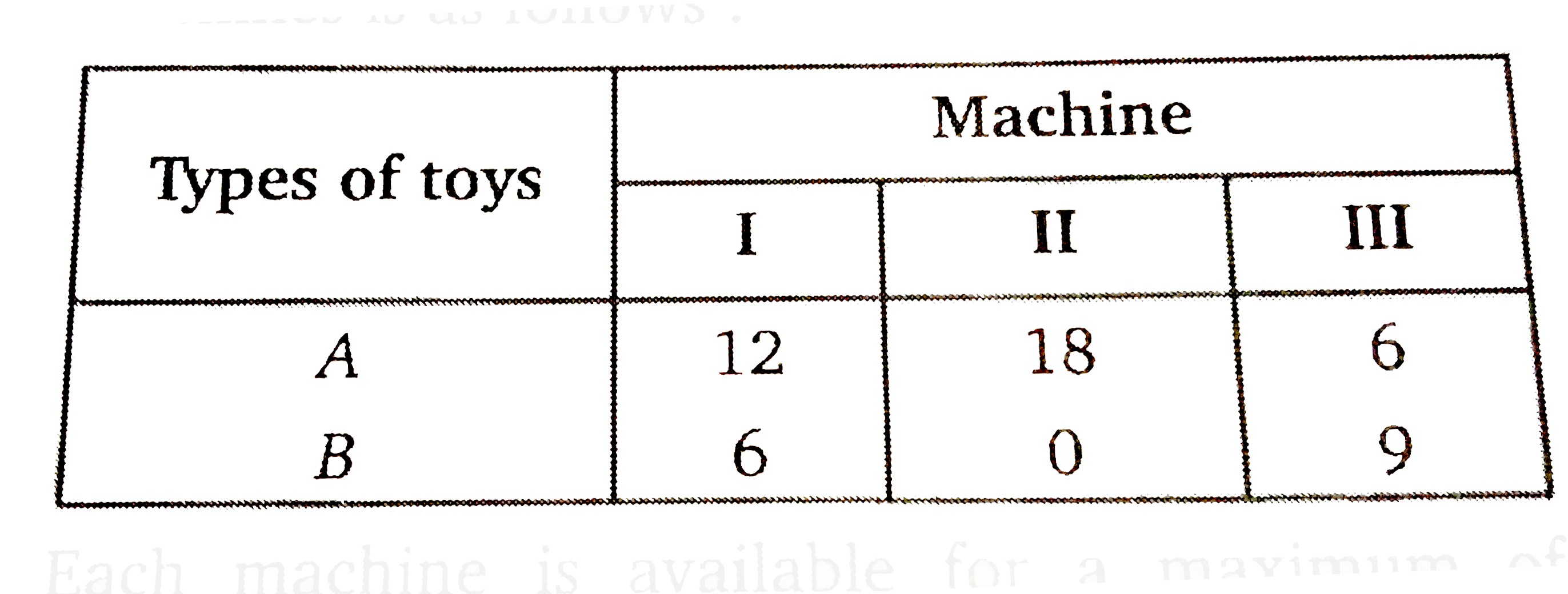 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View SolutionA machine does 392 J of work in 4 seconds. What is the power of the machine?
View Solution
Knowledge Check
A machine gun fires n bullets per second and the mass of each bullet is m. If v is the speed of each bullet, then the force exerted on the machine gun is
Am n gBm n vCm n v gD(m n v )/gThe power output of machine that lifts a 600 kg crate through a height of 20 m in 1 minute, is
A0.98 kWB1.96 kWC3.92 kWD12 kW
A man sold a washing machine for Rs. 13200, thus earning a profit of 10%. Find the cost price of the machine.
View SolutionA firm manufactures two products A and B. Each product is processed on two machines M1andM2 . Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2 . The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs. 3 and Rs. 4 respectively. Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
View SolutionA manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionRaghu has enough money to buy 75 machines worth Rs.200 each. How many machines can he buy if he gets a discount of Rs.50 on each machine ?
View SolutionM, N and P are the mid-points of AB, AC and BC respectively. If MN=3cm, NP=3.5cm and MP=2.5cm , calculate BC, AB and AC
View SolutionA block of mass m kg is kept on a weighing machine in an elevator. If the elevator is retarding upward by a ms−2, the reading of weighing machine is
View Solution
