In fig. 10, A,B,C and D are four points, and no three points are collinear. AC and BD intersect at O. there are eight triangle that you can observe. Name all the triangles.
To solve the problem of naming all the triangles formed by the points A, B, C, and D, which intersect at point O, we will follow these steps:
1. Identify the Points and Intersection:
- We have four points: A, B, C, and D.
- The lines AC and BD intersect at point O.
2. List the Small Triangles:
- First, we can identify the smaller triangles formed by the intersection:
- Triangle BOC (formed by points B, O, and C)
- Triangle COD (formed by points C, O, and D)
- Triangle AOB (formed by points A, O, and B)
- Triangle AOD (formed by points A, O, and D)
3. List the Larger Triangles:
- Next, we can identify the larger triangles that include the smaller ones:
- Triangle ACD (formed by points A, C, and D)
- Triangle ABC (formed by points A, B, and C)
- Triangle BCD (formed by points B, C, and D)
- Triangle ABD (formed by points A, B, and D)
4. Compile the List of Triangles:
- Now we can compile the complete list of triangles:
1. Triangle BOC
2. Triangle COD
3. Triangle AOB
4. Triangle AOD
5. Triangle ACD
6. Triangle ABC
7. Triangle BCD
8. Triangle ABD
Final Answer:
The eight triangles are:
1. Triangle BOC
2. Triangle COD
3. Triangle AOB
4. Triangle AOD
5. Triangle ACD
6. Triangle ABC
7. Triangle BCD
8. Triangle ABD
- We have four points: A, B, C, and D.
- The lines AC and BD intersect at point O.
- First, we can identify the smaller triangles formed by the intersection:
- Triangle BOC (formed by points B, O, and C)
- Triangle COD (formed by points C, O, and D)
- Triangle AOB (formed by points A, O, and B)
- Triangle AOD (formed by points A, O, and D)
- Next, we can identify the larger triangles that include the smaller ones:
- Triangle ACD (formed by points A, C, and D)
- Triangle ABC (formed by points A, B, and C)
- Triangle BCD (formed by points B, C, and D)
- Triangle ABD (formed by points A, B, and D)
- Now we can compile the complete list of triangles:
1. Triangle BOC
2. Triangle COD
3. Triangle AOB
4. Triangle AOD
5. Triangle ACD
6. Triangle ABC
7. Triangle BCD
8. Triangle ABD
The eight triangles are:
1. Triangle BOC
2. Triangle COD
3. Triangle AOB
4. Triangle AOD
5. Triangle ACD
6. Triangle ABC
7. Triangle BCD
8. Triangle ABD
Topper's Solved these Questions
Similar Questions
Take four distinct points, A,B,C and D no three of which are collinear.
Name the line segments.
View SolutionTake four distinct point A,B ,C and D , out of which three points are collinear
Name the line segments.
View SolutionTake four distinct point A,B ,C and D , out of which three points are collinear
Find the number of lines that can be drawn passing through these points.
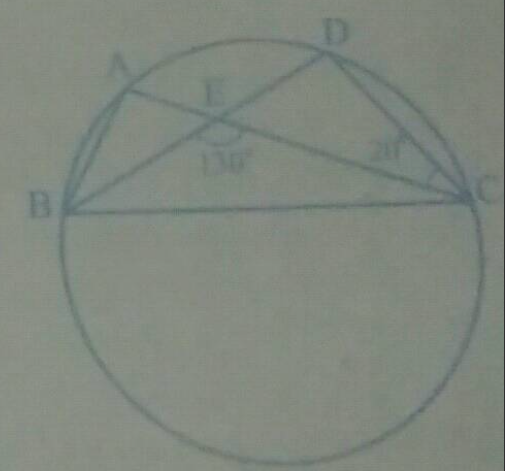
View SolutionIn Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC\ =\ 130o and ∠ECD\ =\ 20⊙ Find ∠BAC.
View SolutionTake four distinct points, A,B,C and D no three of which are collinear.
Find the number of lines that can be drawn passing through these points
View SolutionMark four points A, B, C and D in your notebook such that no three of them are collinear. Draw all the lines which join them in pairs as shown in Fig.
How many such lines can be drawn? Write the names of these lines. Name the lines which are concurrent at A .
View SolutionA, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC =130∘ and ∠ECD=20∘ Find ∠BAC∘
View SolutionIn fig.9, D is a point on side BC of a ABC. AD is joined. Name all the triangle that you can observe in the figure. How many are they?
View SolutionIn fig.9, D is a point on side BC of a ABC. AD is joined. Name all the triangle that you can observe in the figure. How many are they?
View SolutionA,B,C,D are any four points, prove that →AB.→CD+→BC.→AD+→CA.→BD=4(Area of△ABC).
View Solution
