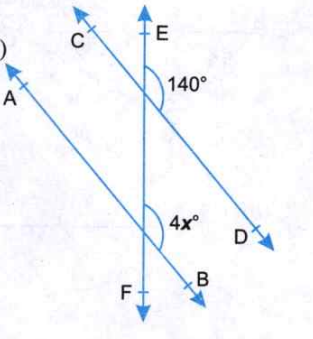
In Fig.98, If AB is parallel to CD and EF is a transversal, then x= (a) 19 (b) 29 (c) 39 (d) 49
To solve the problem step by step, we will use the properties of parallel lines and transversals.
1. Identify the Angles: Given that AB is parallel to CD and EF is a transversal, we can identify the angles formed by the transversal with the two parallel lines. Let's denote the angles as follows:
- Angle 1 = 7x−12
- Angle 2 = 4x+17
2. Use the Co-Interior Angles Property: Since AB is parallel to CD and EF is the transversal, the angles on the same side of the transversal (Angle 1 and Angle 2) are co-interior angles. According to the property of co-interior angles, their sum is equal to 180 degrees.
(7x−12)+(4x+17)=180
3. Combine Like Terms: Now, we will combine the like terms in the equation.
7x+4x−12+17=180
11x+5=180
4. Isolate the Variable: Next, we will isolate x by subtracting 5 from both sides of the equation.
11x=180−5
11x=175
5. Solve for x: Finally, divide both sides by 11 to find the value of x.
x=17511
x≈15.91
6. Check the Options: The calculated value of x is approximately 15.91, which does not match any of the provided options (19, 29, 39, 49). Therefore, it seems there might be an error in the options provided.
Final Answer:
The value of x is approximately 15.91, which is not listed among the options.
- Angle 1 = 7x−12
- Angle 2 = 4x+17
(7x−12)+(4x+17)=180
7x+4x−12+17=180
11x+5=180
11x=180−5
11x=175
x=17511
x≈15.91
The value of x is approximately 15.91, which is not listed among the options.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, AB is parallel to CD. What is the value of x?
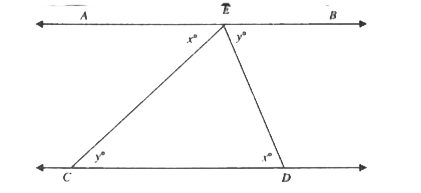 A36B45C60DCannot be determined
A36B45C60DCannot be determined
In Fig. AB∣∣DC . Find the value of x
View SolutionIn Fig. if AB∣∣CD , find the value of x .
View SolutionIn Fig.111, if ABCD then x= (a) 154 (b) 139 (c) 144 (d) 164
View SolutionIn each of the following figures, AB∣∣CD and EF is a transversal. Find the value of x in each case
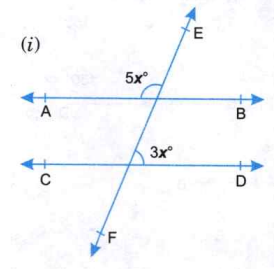
View SolutionIn each of the following figures, AB∣∣CD and EF is a transversal. Find the value of x in each case
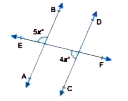
View SolutionIn each of the following figures, AB∣∣CD and EF is a transversal. Find the value of x in each case
View SolutionIf 47 of 49% of x is 21, then x=
(a) 125
(b) 98
(c) 84
(d) 75
View Solution