Question

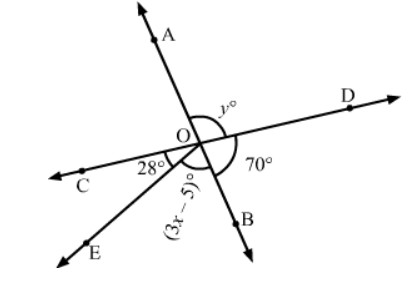
In Fig.113, if$AC\left|\left|DFandAB\right|\right|CE,$
then
(a) $x=145,y=223$
(b) $x=223,y=145$
(c) $x=135,y=223$
(d) $x=233,y=135$

Explanation

To solve the question, we need to determine the values of $$x$$ and $$y$$ given the parallel lines and the angles formed by them.

1. Identify the Given Information:
We have two pairs of parallel lines: \( AC \parallel DF \) and \( AB \parallel CE \). This means that the angles formed by these lines will have specific relationships.

2. Use the Properties of Parallel Lines:
When two lines are parallel, the corresponding angles and alternate interior angles are equal. We will use this property to find the values of \( x \) and \( y \).

3. Set Up the Equations:
Let's assume that angle \( y \) is formed by line \( AB \) and line \( CE \). Since \( AB \parallel CE \), we can say:
\( y + 70 = 180 \quad \text{(since they are supplementary)} \)
From this, we can solve for \( y \):
\( y = 180 - 70 = 110 \)

4. Find the Value of \( x \):
Now, we consider the straight line \( COD \). The angles on this line are \( 70 \), \( 28 \), and \( 3x - 5 \). Since \( COD \) is a straight line, we can write:
\( 70 + 28 + (3x - 5) = 180 \)
Simplifying this equation gives:
\( 3x + 70 + 28 - 5 = 180 \)
\( 3x + 93 = 180 \)
Now, subtract \( 93 \) from both sides:
\( 3x = 180 - 93 = 87 \)
Dividing by \( 3 \):
\( x = \frac{87}{3} = 29 \)

5. Final Values:
We have found:
\( x = 29 \quad \text{and} \quad y = 110 \)

Conclusion:
The correct option is (c) \( x = 29 \) and \( y = 110 \).