The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the: (i) Highest and the lowest marks obtained by the students. (ii) Range of the marks obtained. (iii) Mean marks obtain
To solve the question step by step, we will find the highest and lowest marks, the range of the marks, and the mean marks obtained by the students.
Step 1: Identify the highest and lowest marks
1. List the marks: The marks obtained by the students are:
- 85, 76, 90, 85, 39, 48, 56, 95, 81, 75
2. Find the highest mark: Look for the maximum value in the list.
- The highest mark is 95.
3. Find the lowest mark: Look for the minimum value in the list.
- The lowest mark is 39.
Step 2: Calculate the range of the marks
1. Use the formula for range:
Range=Highest mark−Lowest mark
2. Substitute the values:
Range=95−39
3. Perform the calculation:
Range=56
Step 3: Calculate the mean marks
1. Sum all the marks:
Sum=85+76+90+85+39+48+56+95+81+75
- Calculate the sum:
- 85+76=161
- 161+90=251
- 251+85=336
- 336+39=375
- 375+48=423
- 423+56=479
- 479+95=574
- 574+81=655
- 655+75=730
- Therefore, the total sum of marks is 730.
2. Count the number of students: There are 10 students.
3. Use the formula for mean:
Mean=Sum of marksNumber of students=73010
4. Perform the division:
Mean=73
Final Answers
(i) Highest marks = 95, Lowest marks = 39
(ii) Range of marks = 56
(iii) Mean marks = 73
1. List the marks: The marks obtained by the students are:
- 85, 76, 90, 85, 39, 48, 56, 95, 81, 75
2. Find the highest mark: Look for the maximum value in the list.
- The highest mark is 95.
3. Find the lowest mark: Look for the minimum value in the list.
- The lowest mark is 39.
1. Use the formula for range:
Range=Highest mark−Lowest mark
2. Substitute the values:
Range=95−39
3. Perform the calculation:
Range=56
1. Sum all the marks:
Sum=85+76+90+85+39+48+56+95+81+75
- Calculate the sum:
- 85+76=161
- 161+90=251
- 251+85=336
- 336+39=375
- 375+48=423
- 423+56=479
- 479+95=574
- 574+81=655
- 655+75=730
- Therefore, the total sum of marks is 730.
2. Count the number of students: There are 10 students.
3. Use the formula for mean:
Mean=Sum of marksNumber of students=73010
4. Perform the division:
Mean=73
(i) Highest marks = 95, Lowest marks = 39
(ii) Range of marks = 56
(iii) Mean marks = 73
Topper's Solved these Questions
Similar Questions
The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
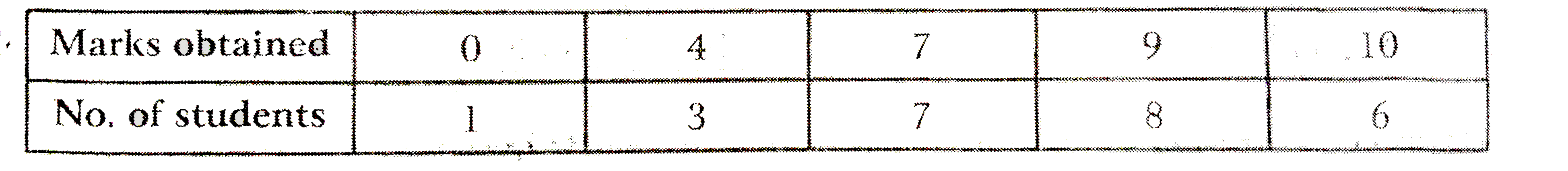
View SolutionThe marks obtained (out of 100) by 12 students in an examination are
74, 96, 87, 65, 99, 82, 76, 92, 66, 75, 85, 90
Find the median marks.
View SolutionThe percentage of marks obtained by students of a class in mathematics are: 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
View SolutionThe percentage of marks obtained by students of a class in mathematics are: 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
View SolutionThe marks obtained (out of 30) by five students in a test are 20, 15, 25, 18, and 22. Find the average marks obtained.
View SolutionFind out the mode of the following marks obtained by 15 students in a class: Marks: 4, 6, 5, 7, 9, 8, 10, 4, 7, 6, 5, 9, 8, 7, 7
View SolutionThe marks obtained by 30 students of Class X of a certain school in a Mathematics paper consisting of 100 marks are presented in table below. Find the mean of the marks obtained by the students.
View SolutionThe marks obtained by 12 students in an examination (out of 50) are given below:
18, 35, 2, 27, 40, 0, 21, 33, 27, 8, 36, 23
Find the mean marks.
View SolutionIf for somex∈R, the frequency distribution of the marks obtained by 20 students in a test is:

Then the mean of the marks is:
View SolutionFollowing are the marks obtained by 9 student in a mathematics test
50,69,20,33,53,39,40,65,59,
The mean deviation from the median is
View Solution
