Solve each of the following Cryptarithms: (i)
To solve the cryptarithm A1+1B=B0, we will follow these steps:
Step 1: Understand the Structure of the Numbers
The expression A1 represents the two-digit number where A is the tens digit and 1 is the units digit. Similarly, 1B represents another two-digit number where 1 is the tens digit and B is the units digit. The result B0 represents a two-digit number where B is the tens digit and 0 is the units digit.
Step 2: Set Up the Equation
We can express the numbers in terms of A and B:
- A1=10A+1
- 1B=10+B
- B0=10B+0
Now, we can rewrite the equation:
(10A+1)+(10+B)=10B
Step 3: Simplify the Equation
Combine like terms:
10A+1+10+B=10B
10A+11+B=10B
Step 4: Rearrange the Equation
Now, we can rearrange the equation to isolate terms involving B:
10A+11=10B−B
10A+11=9B
Step 5: Solve for B
From the equation 10A+11=9B, we can express B in terms of A:
B=10A+119
Step 6: Determine Possible Values for A and B
Since A and B must be single-digit integers (0-9), we can test values of A from 0 to 9 to find valid integer values for B.
- For A=0: B=10(0)+119=119 (not an integer)
- For A=1: B=10(1)+119=219 (not an integer)
- For A=2: B=10(2)+119=319 (not an integer)
- For A=3: B=10(3)+119=419 (not an integer)
- For A=4: B=10(4)+119=519 (not an integer)
- For A=5: B=10(5)+119=619 (not an integer)
- For A=6: B=10(6)+119=719 (not an integer)
- For A=7: B=10(7)+119=819=9 (valid)
- For A=8: B=10(8)+119=919 (not an integer)
- For A=9: B=10(9)+119=1019 (not an integer)
Step 7: Final Values
The only valid pair we found is A=7 and B=9.
Conclusion
Thus, the solution to the cryptarithm is:
- A=7
- B=9
The expression A1 represents the two-digit number where A is the tens digit and 1 is the units digit. Similarly, 1B represents another two-digit number where 1 is the tens digit and B is the units digit. The result B0 represents a two-digit number where B is the tens digit and 0 is the units digit.
We can express the numbers in terms of A and B:
- A1=10A+1
- 1B=10+B
- B0=10B+0
(10A+1)+(10+B)=10B
Combine like terms:
10A+1+10+B=10B
10A+11+B=10B
Now, we can rearrange the equation to isolate terms involving B:
10A+11=10B−B
10A+11=9B
From the equation 10A+11=9B, we can express B in terms of A:
B=10A+119
Since A and B must be single-digit integers (0-9), we can test values of A from 0 to 9 to find valid integer values for B.
- For A=1: B=10(1)+119=219 (not an integer)
- For A=2: B=10(2)+119=319 (not an integer)
- For A=3: B=10(3)+119=419 (not an integer)
- For A=4: B=10(4)+119=519 (not an integer)
- For A=5: B=10(5)+119=619 (not an integer)
- For A=6: B=10(6)+119=719 (not an integer)
- For A=7: B=10(7)+119=819=9 (valid)
- For A=8: B=10(8)+119=919 (not an integer)
- For A=9: B=10(9)+119=1019 (not an integer)
The only valid pair we found is A=7 and B=9.
Thus, the solution to the cryptarithm is:
- A=7
- B=9
Topper's Solved these Questions
Similar Questions
Solve the following cryptarithms :
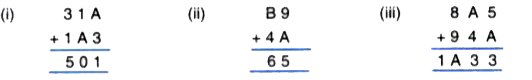
View SolutionSolve the following cryptarithms: ABx6=BBB
View SolutionSolve the following cryptarithms: 37+AB=9A
View SolutionFind the solution for following cryptarithms:
ABx3=CAB
View SolutionSolve each of the following equations :
a2x2−b2=0
View SolutionEvaluate each of the following using identities:
(i)(a2b−b2a)2
(ii) (a−0.1)(a+0.1)
View SolutionSolve the cryptarithm: AB X AB= ACB
View SolutionSolve the cryptarithm: BAXB3=57A
View SolutionEvaluate of each of the following integrals (1-15): ∫a−a11+axdx,a>0
View SolutionProve that the value of each the following determinants is zero: ∣∣ ∣∣a1la1+mb1b1a2la2+mb2b2a3la3+mb3b3∣∣ ∣∣
View Solution
