Question

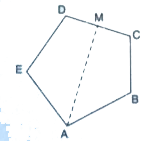
$ABCDE$
is a regular pentagon. The bisector of $\angle A$
of the pentagon meets the side $CD$
in $M\stackrel{.}{}$
Show that $\angle AMC={90}^0\stackrel{.}{}$

Answer

`/_AMC=90^@`

Explanation

To solve the problem, we need to show that the angle $$\angle AMC$$ is equal to $${90}^{\circ }$$ in the regular pentagon $$ABCDE$$.

1. Understanding the Regular Pentagon:
A regular pentagon has all sides equal and all interior angles equal. The number of sides \( N \) for a pentagon is 5.

2. Calculating Each Interior Angle:
The formula for calculating the interior angle of a polygon is:
\( \text{Interior Angle} = \frac{(N - 2) \times 180^\circ}{N} \)
For a pentagon:
\( \text{Interior Angle} = \frac{(5 - 2) \times 180^\circ}{5} = \frac{3 \times 180^\circ}{5} = \frac{540^\circ}{5} = 108^\circ \)
Thus, each interior angle of the pentagon \( ABCDE \) is \( 108^\circ \).

3. Finding the Angle Bisector:
The bisector of angle \( A \) divides \( \angle A \) into two equal parts. Therefore:
\( \angle MAB = \angle MAC = \frac{108^\circ}{2} = 54^\circ \)

4. Analyzing Quadrilateral \( ABMC \):
In quadrilateral \( ABMC \), the sum of the interior angles is \( 360^\circ \). Therefore:
\( \angle MAB + \angle B + \angle C + \angle AMC = 360^\circ \)
Substituting the known angles:
\( 54^\circ + 108^\circ + 108^\circ + \angle AMC = 360^\circ \)

5. Calculating \( \angle AMC \):
Now, we can simplify the equation:
\( 54^\circ + 216^\circ + \angle AMC = 360^\circ \)
\( 270^\circ + \angle AMC = 360^\circ \)
\( \angle AMC = 360^\circ - 270^\circ = 90^\circ \)

6. Conclusion:
Thus, we have shown that:
\( \angle AMC = 90^\circ \)