A vessel A has volume V and a vessel B has volume 2V. Both contain some water which has constant volume. The pressure in the space above water is pa for vessel A and pb for vessel B.
(a)pa=pb
(b)pa=2pb
(c)pb=2pa
(d)pb=4pa
The correct Answer is:A
To solve the problem, we need to analyze the situation in both vessels A and B, considering the properties of the water and the vapor above it.
1. Understanding the Setup:
- Vessel A has a volume V and vessel B has a volume 2V.
- Both vessels contain water, which has a constant volume, meaning the amount of water does not change.
2. Identifying the Pressures:
- The pressure in the space above the water in vessel A is denoted as pA.
- The pressure in the space above the water in vessel B is denoted as pB.
3. Saturation Condition:
- Since both vessels contain water, the vapor above the liquid in both vessels will reach a state of saturation.
- In a saturated state, the number of molecules transitioning from the liquid to the vapor phase is equal to the number returning from the vapor to the liquid phase.
4. Constant Volume Implication:
- The constant volume of water in both vessels implies that the vapor pressure above the liquid must also be constant.
- This means that the vapor pressure in both vessels must be equal because they are both in a saturated state.
5. Conclusion:
- Since both pA and pB represent the saturated vapor pressure above the water in their respective vessels, we can conclude that:
pA=pB
Final Answer:
Thus, the relationship between the pressures in the two vessels is:
pA=pB
- Vessel A has a volume V and vessel B has a volume 2V.
- Both vessels contain water, which has a constant volume, meaning the amount of water does not change.
- The pressure in the space above the water in vessel A is denoted as pA.
- The pressure in the space above the water in vessel B is denoted as pB.
- Since both vessels contain water, the vapor above the liquid in both vessels will reach a state of saturation.
- In a saturated state, the number of molecules transitioning from the liquid to the vapor phase is equal to the number returning from the vapor to the liquid phase.
- The constant volume of water in both vessels implies that the vapor pressure above the liquid must also be constant.
- This means that the vapor pressure in both vessels must be equal because they are both in a saturated state.
- Since both pA and pB represent the saturated vapor pressure above the water in their respective vessels, we can conclude that:
pA=pB
Thus, the relationship between the pressures in the two vessels is:
pA=pB
Topper's Solved these Questions
Similar Questions
When a gas is heated in a vessel of constant volume , the pressure increases because
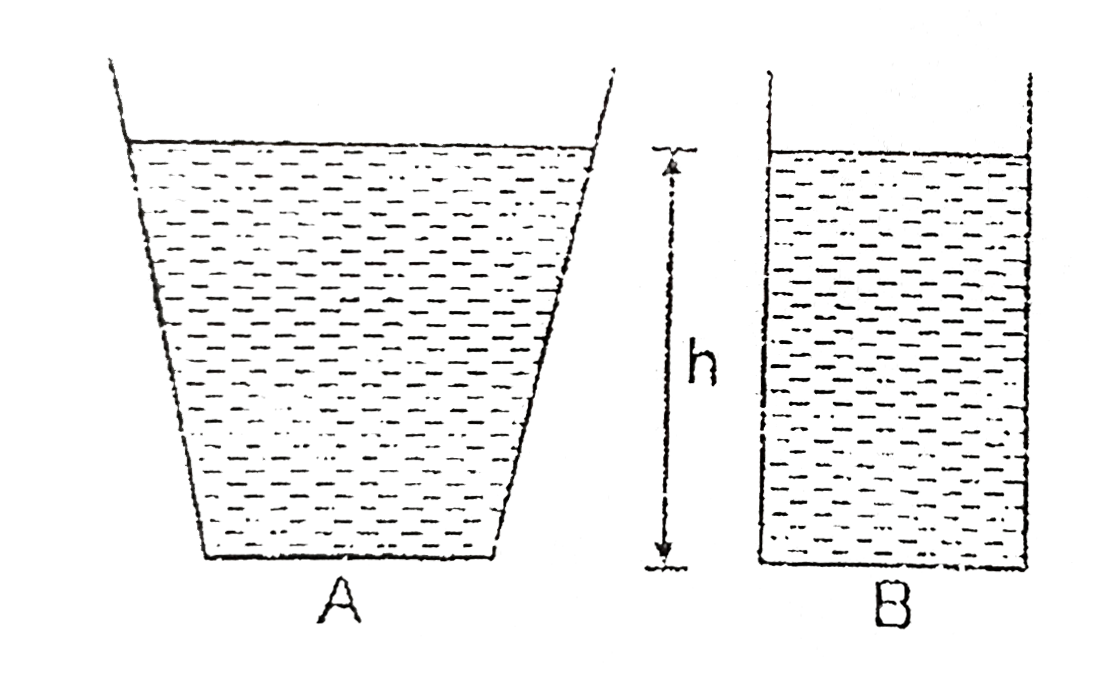
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
View Solution2g of hydrogen is sealed in a vessel of volume 0.02m3and is maintained at 300K. Calculate the pressure in the vessel.
View SolutionA vessel of volume 3V contains a gas at pressure 4P0 and another vessel of volume 2V contains same gas at pressure 1.5P0. Both vessels have same temperature. When both vessels are connected by a tube of negligible volume, the equilibrium is IP0, where I is an integer. Find the value of I.
View SolutionA closed vessel A having volume V contains N2 at pressure P and temperature T. another closed vessel B having the same volume V contains. He at the same pressure P. but temperature 2T. The ratio of masses of N2 and He in the vesses A and B is
View SolutionA gas is enclosed in a vessel of volume V at a pressure P. It is being pumped out of the vessel by mean of a piston-pump with a stroke volume. v. What is the final pressure in the vessel after 'n' strokes of the pump ? Assume temperature reamains constant.
View SolutionThe volume of a given mass of a gas in a vessel is reduced to half at constant temperature what is the change in pressure?
View SolutionA vessel of volume V0 contains an ideal gas at pressure p0and temperature T. Gas is continuously pumped out of this vessel at a constant volume-rate dVdt=r keeping the temperature constant, The pressure inside the vessel. Find (a) the pressure of the gas as a function of time,(b) the time taken before half the original gas is pumped out.
View SolutionEqual masses of air are sealed in two vessels, one if volume V0and the other of volume 2V0.If the first vessel is maintained at a temperature 300K and the other at 600K, find the ratio of the pressures in the two vessels.
View SolutionTwo vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View Solution
