A closed vessel A having volume V contains N2 at pressure P and temperature T. another closed vessel B having the same volume V contains. He at the same pressure P. but temperature 2T. The ratio of masses of N2 and He in the vesses A and B is
1:2
3:2
5:2
14:1
The correct Answer is:D
To solve the problem, we need to find the ratio of the masses of nitrogen (N₂) in vessel A and helium (He) in vessel B. We will use the ideal gas law and the relationship between moles, mass, and molecular mass.
1. Identify Given Data:
- For vessel A (N₂):
- Volume (V) = V
- Pressure (P) = P
- Temperature (T) = T
- For vessel B (He):
- Volume (V) = V
- Pressure (P) = P
- Temperature (T) = 2T
2. Use the Ideal Gas Law:
The ideal gas law is given by:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature
3. Calculate Moles for Each Gas:
- For nitrogen (N₂) in vessel A:
n1=PVRT
Substituting T=T:
n1=PVRT
- For helium (He) in vessel B:
n2=PVR(2T)
Substituting T=2T:
n2=PV2RT
4. Relate the Moles:
From the equations for n1 and n2:
n1=PVRTandn2=PV2RT
We can express n1 in terms of n2:
n1=2n2
5. Relate Mass to Moles:
The mass of a gas can be expressed as:
mass=n×molecular mass
Therefore, for nitrogen (N₂):
mN2=n1×MN2
And for helium (He):
mHe=n2×MHe
6. Substituting Moles into Mass Equations:
Substitute n1 and n2:
mN2=(2n2)×MN2
mHe=n2×MHe
7. Calculate the Ratio of Masses:
Now, we can find the ratio of the masses:
mN2mHe=(2n2)×MN2n2×MHe=2MN2MHe
8. Substituting Molecular Masses:
The molecular mass of nitrogen MN2=28g/mol and for helium MHe=4g/mol:
mN2mHe=2×284=564=14
9. Final Ratio:
Thus, the ratio of the masses of nitrogen to helium is:
mN2mHe=14:1
Conclusion:
The ratio of the masses of N2 and He in the vessels A and B is 14:1.
- For vessel A (N₂):
- Volume (V) = V
- Pressure (P) = P
- Temperature (T) = T
- For vessel B (He):
- Volume (V) = V
- Pressure (P) = P
- Temperature (T) = 2T
The ideal gas law is given by:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature
- For nitrogen (N₂) in vessel A:
n1=PVRT
Substituting T=T:
n1=PVRT
n2=PVR(2T)
Substituting T=2T:
n2=PV2RT
From the equations for n1 and n2:
n1=PVRTandn2=PV2RT
We can express n1 in terms of n2:
n1=2n2
The mass of a gas can be expressed as:
mass=n×molecular mass
Therefore, for nitrogen (N₂):
mN2=n1×MN2
And for helium (He):
mHe=n2×MHe
Substitute n1 and n2:
mN2=(2n2)×MN2
mHe=n2×MHe
Now, we can find the ratio of the masses:
mN2mHe=(2n2)×MN2n2×MHe=2MN2MHe
The molecular mass of nitrogen MN2=28g/mol and for helium MHe=4g/mol:
mN2mHe=2×284=564=14
Thus, the ratio of the masses of nitrogen to helium is:
mN2mHe=14:1
The ratio of the masses of N2 and He in the vessels A and B is 14:1.
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-B) Objective type questions (One option is correct)
10 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-C) Objective type questions (More than one option are correct)
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Try Yourself
43 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionThe pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed vessel A and B of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a naroow open tube. If th temperature of one is now maintained at T1 and other at T2 (wehre T1>T2 ) then that what will be the final pressure ?
View SolutionA vessel of volume 3V contains a gas at pressure 4P0 and another vessel of volume 2V contains same gas at pressure 1.5P0. Both vessels have same temperature. When both vessels are connected by a tube of negligible volume, the equilibrium is IP0, where I is an integer. Find the value of I.
View SolutionTwo gases A and B having the same pressure P, volume V and temperature T are mixed. If mixture has volume and temperature as V and T respectively, then the pressure of the mixture will be
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
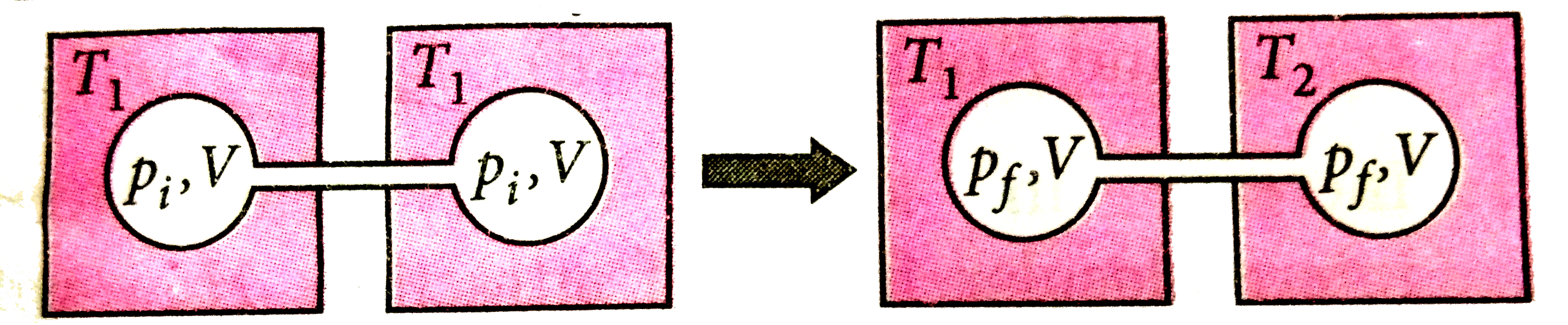
View Solution
