Let →Aand→B be the two vectors of magnitude 10 unit each. If they are inclined to the X-axis at angles 30∘and60∘ respectively, find the resultant.
The correct Answer is:19.3
To find the resultant of the two vectors →A and →B with magnitudes of 10 units each and angles of 30∘ and 60∘ with the x-axis respectively, we can follow these steps:
Step 1: Determine the components of each vector
The components of a vector can be found using trigonometric functions. For vector →A and →B:
- The x-component of →A:
Ax=Acos(30∘)=10cos(30∘)=10⋅√32=5√3
- The y-component of →A:
Ay=Asin(30∘)=10sin(30∘)=10⋅12=5
- The x-component of →B:
Bx=Bcos(60∘)=10cos(60∘)=10⋅12=5
- The y-component of →B:
By=Bsin(60∘)=10sin(60∘)=10⋅√32=5√3
Step 2: Calculate the resultant components
Now, we can find the resultant vector →R by summing the components of →A and →B:
- Resultant x-component:
Rx=Ax+Bx=5√3+5
- Resultant y-component:
Ry=Ay+By=5+5√3
Step 3: Calculate the magnitude of the resultant vector
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
R=√R2x+R2y
Substituting the values:
R=√(5√3+5)2+(5+5√3)2
Calculating each term:
1. R2x=(5√3+5)2=(5√3)2+2⋅5√3⋅5+52=75+50√3+25=100+50√3
2. R2y=(5+5√3)2=52+2⋅5⋅5√3+(5√3)2=25+50√3+75=100+50√3
Now, adding these:
R2=(100+50√3)+(100+50√3)=200+100√3
Finally, taking the square root:
R=√200+100√3
Step 4: Approximate the value
Using √3≈1.732:
R≈√200+100⋅1.732=√200+173.2=√373.2
Thus, the resultant vector →R is approximately:
R≈19.3 units
Final Answer
The magnitude of the resultant vector →R is approximately 19.3 units.
The components of a vector can be found using trigonometric functions. For vector →A and →B:
Ax=Acos(30∘)=10cos(30∘)=10⋅√32=5√3
Ay=Asin(30∘)=10sin(30∘)=10⋅12=5
Bx=Bcos(60∘)=10cos(60∘)=10⋅12=5
By=Bsin(60∘)=10sin(60∘)=10⋅√32=5√3
Now, we can find the resultant vector →R by summing the components of →A and →B:
Rx=Ax+Bx=5√3+5
Ry=Ay+By=5+5√3
The magnitude of the resultant vector →R can be calculated using the Pythagorean theorem:
R=√R2x+R2y
R=√(5√3+5)2+(5+5√3)2
1. R2x=(5√3+5)2=(5√3)2+2⋅5√3⋅5+52=75+50√3+25=100+50√3
2. R2y=(5+5√3)2=52+2⋅5⋅5√3+(5√3)2=25+50√3+75=100+50√3
R2=(100+50√3)+(100+50√3)=200+100√3
R=√200+100√3
Using √3≈1.732:
R≈√200+100⋅1.732=√200+173.2=√373.2
R≈19.3 units
The magnitude of the resultant vector →R is approximately 19.3 units.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 25videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
Similar Questions
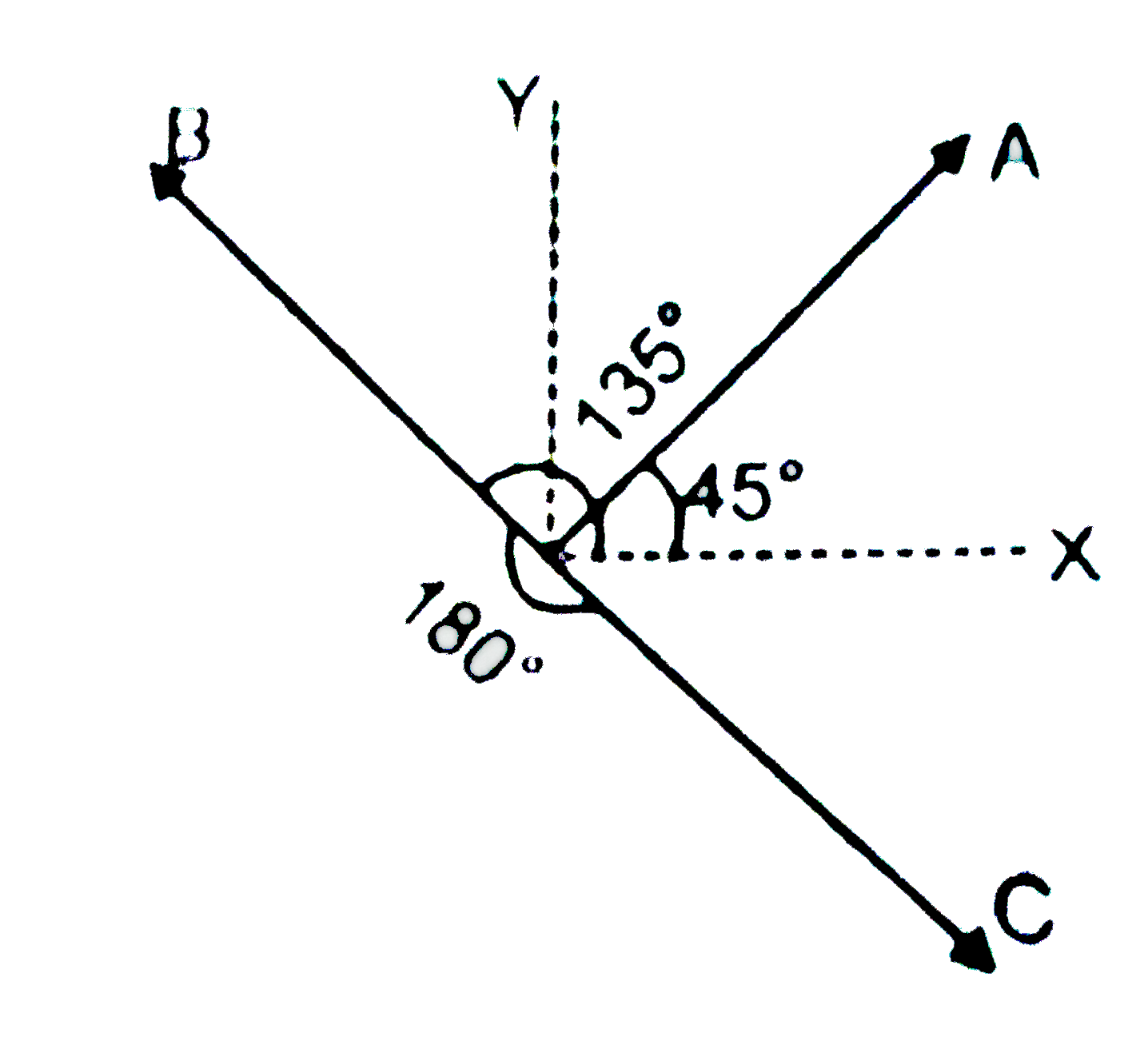
Add vectors →A,→Band→C each having magnitude of 100 unit and inclined to the X-axis at angles 45∘,135∘and315∘ respectively.
View SolutionIf →aand→b are unit vectors inclined to x-axis at angle 30∘and120∘ then ∣∣→a+→b∣∣ equals
View SolutionIf →aand→b are two vectors of magnitude 1 inclined at 120∘, then find the angle between →band→b−→a.
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
 View Solution
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
 View Solution
View SolutionLet →a and →b be two vectors of the same magnitude such that the angle between them is 60∘ and →a.→b=8. Find |→a| and ∣∣→b∣∣.
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of −−→110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionTwo vectors having magnitude 12 and 13 are inclined at and angle45∘ to each other.find their resultant vector.
View SolutionLet →a and →b are unit vectors inclined at an angle α to each other , if ∣∣→a+→b∣∣<1 then
View SolutionLet →aand→b be two unit vectors and α be the angle between them, then →a+→b is a unit vector , if α =
View Solution

