The accleration of a particle as seen from two frames S1 and S2 have equal magnitudes 4 m/s2
The frames must be at rest with respect to each other.
The frames may be moves with respect to each other but neigther should be accelerates with respect to the other.
The acceleration of S2 with respect to S1 may either be zero or 8 m/s^2.
The acceleration of S2 with respect to S1 may be anything between zero and 8ms2
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the accelerations of a particle as seen from two different frames of reference, S1 and S2, both of which observe the particle having an acceleration of equal magnitude, 4m/s2.
1. Understanding the Problem:
- We have two frames of reference, S1 and S2.
- Both frames observe a particle with an acceleration of 4m/s2.
2. Acceleration in Different Frames:
- The acceleration of the particle as seen from frame S1 is aP/S1=4m/s2.
- The acceleration of the particle as seen from frame S2 is aP/S2=4m/s2.
3. Relative Acceleration:
- The relative acceleration of frame S2 with respect to frame S1 can be expressed using the formula:
aP/S1=aP/S2+aS2/S1
- Rearranging gives us:
aS2/S1=aP/S1−aP/S2
4. Calculating the Range of Relative Acceleration:
- Since both aP/S1 and aP/S2 are equal to 4m/s2, we can substitute:
aS2/S1=4−4=0m/s2
- However, the direction of the accelerations can vary. The angle between the two acceleration vectors can range from 0∘ to 180∘.
5. Using Vector Addition:
- The maximum possible relative acceleration occurs when the two accelerations are in opposite directions (180 degrees apart):
aS2/S1=4+4=8m/s2
- Therefore, the relative acceleration aS2/S1 can range from 0m/s2 to 8m/s2.
6. Conclusion:
- The acceleration of S2 with respect to S1 can take any value between 0m/s2 and 8m/s2.
Final Answer:
The correct option is Option 4: The acceleration of S2 with respect to S1 may be anything between 0 and 8m/s2.
- We have two frames of reference, S1 and S2.
- Both frames observe a particle with an acceleration of 4m/s2.
- The acceleration of the particle as seen from frame S1 is aP/S1=4m/s2.
- The acceleration of the particle as seen from frame S2 is aP/S2=4m/s2.
- The relative acceleration of frame S2 with respect to frame S1 can be expressed using the formula:
aP/S1=aP/S2+aS2/S1
- Rearranging gives us:
aS2/S1=aP/S1−aP/S2
- Since both aP/S1 and aP/S2 are equal to 4m/s2, we can substitute:
aS2/S1=4−4=0m/s2
- However, the direction of the accelerations can vary. The angle between the two acceleration vectors can range from 0∘ to 180∘.
- The maximum possible relative acceleration occurs when the two accelerations are in opposite directions (180 degrees apart):
aS2/S1=4+4=8m/s2
- Therefore, the relative acceleration aS2/S1 can range from 0m/s2 to 8m/s2.
- The acceleration of S2 with respect to S1 can take any value between 0m/s2 and 8m/s2.
The correct option is Option 4: The acceleration of S2 with respect to S1 may be anything between 0 and 8m/s2.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -1
13 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
Velocity and acceleration of a particle are v=(2ˆi−4ˆj)ms and a=(−2ˆi+4ˆj)ms2 Which type of motion is this?
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionA particle is found to be at rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. Select the possible options :
View SolutionStatement I: A particle is found to be a rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. We can say both the frames are inertial.
Statement II: All frames moving uniformly with respect to an inertial frame are themselves inertial.
View SolutionThe body moves along the x−axis . At time t=0 the velocity of particle is +0.5m/s. The acceleration of particle in different time interval is given as:
a=⎧⎪ ⎪⎨⎪ ⎪⎩−1m/s2 0s≤t≤3s−2m/s2 3s<t<6s+4m/s2 6s≤t≤10s
View SolutionA particle is found to be at rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2
(a) Both the frames are inertial
(b) Both the frames are non inertial
(c ) S1 is inertial and S2 is non inertial
(d) S1 is non inertial and S2 is inertial
View SolutionA particle is found to be at rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2
a) Both the frames are inertial
b) Both the frames are non inertial
c) S1 is inertial and S2 is non inertial
d) S1 is non inertial and S2 is inertial
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
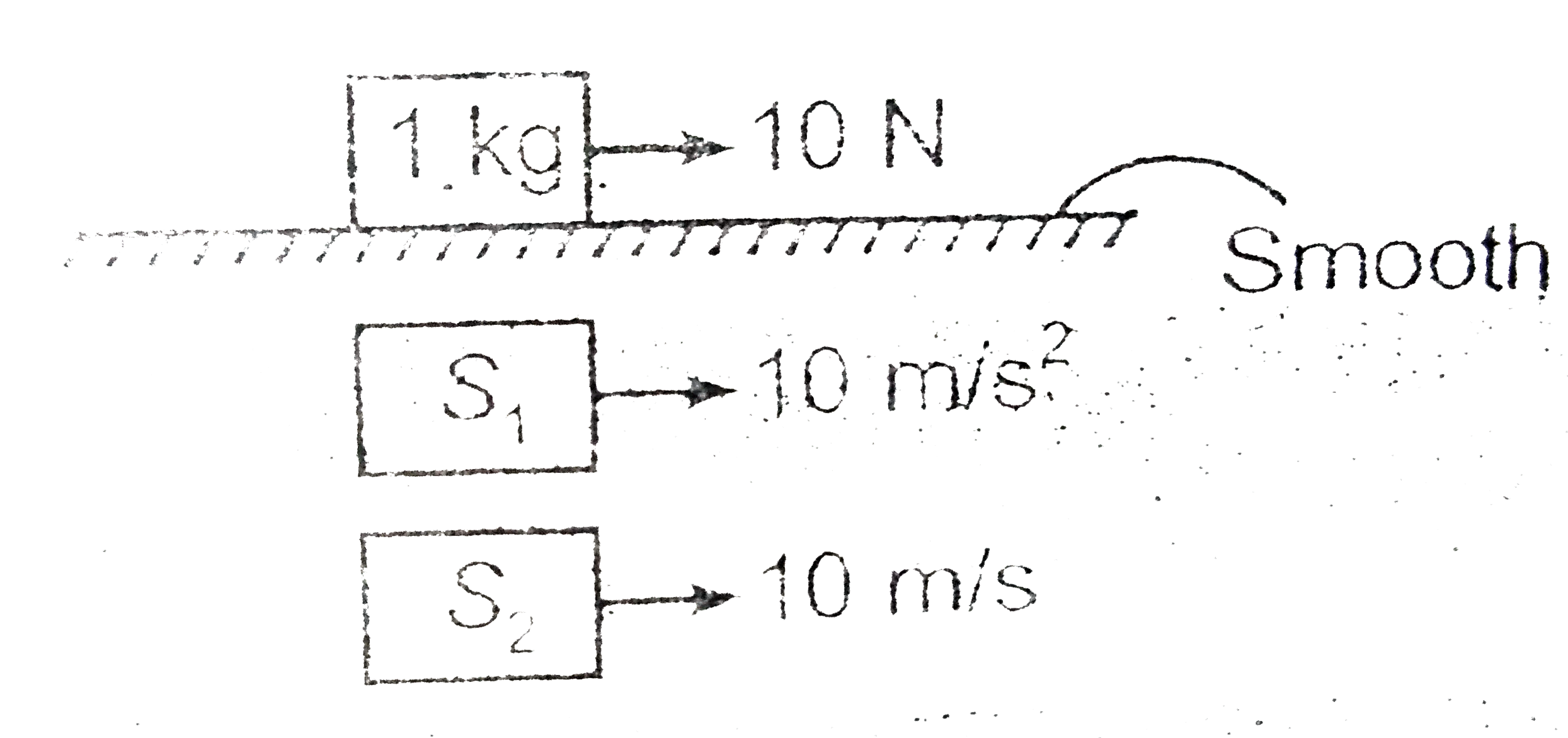
The rate at which work is done by constant force on the particle is always non-negative when observed fom
View SolutionCalculate the magnitude and direction of total linear acceleration of a particle moving in a circle of radius 0.4 m having an instantaneous angular velocity of 2rads−1 and angular acceleration 5"rad"s^(-2)
View SolutionTwo sources of sound S1 and S2 produce sound waves of same frequency 660Hz. A listener is moving from source S1 towards S2 with a constant speed um/s and he hears 10 beats/s. The velocity of sound is 330m/s. Then, u equals :
View Solution
