An aeroplane has to go from a point A to another point B, away due east of north. Wind is blowing due north at a speed of The air-speed of the plane is (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.
The correct Answer is:A, B
To solve this problem, we will break it down into two parts:
Part (a): Finding the Direction in Which the Pilot Should Head the Plane
1. Understanding the Problem:
- The distance from point A to point B is 500 km at an angle of 30° east of north.
- The wind is blowing due north at a speed of 20 m/s.
- The airspeed of the plane is 150 m/s.
2. Setting Up the Coordinate System:
- Let’s define the north direction as the positive y-axis and the east direction as the positive x-axis.
- The angle of 30° east of north means that the direction from A to B can be represented in vector form.
3. Calculating the Components of the Velocity:
- The velocity of the wind (V_wind) is purely in the y-direction:
Vwind=20m/s^j
- The velocity of the plane (V_plane) can be broken down into components based on the angle α (the angle the pilot should head):
Vplane=150m/s(cosα^i+sinα^j)
4. Finding the Resultant Velocity:
- The resultant velocity of the plane with respect to the ground (V_g) must point towards B:
Vg=Vplane+Vwind
- The x-component of V_g must be equal to the x-component of the direction to B, and the y-component must balance the wind.
5. Setting Up the Equations:
- The angle to B gives us:
tan(30°)=VygVxg
- The y-component of V_g:
Vyg=150sinα+20
- The x-component of V_g:
Vxg=150cosα
6. Using the Tangent Function:
- From the angle:
tan(30°)=1√3=150sinα+20150cosα
- Rearranging gives:
150sinα+20=150cosα√3
7. Solving for α:
- Rearranging and substituting known values allows us to isolate and solve for sin(α) and cos(α).
- After calculations, we find:
sinα=115⟹α=sin−1(115)
Part (b): Finding the Time Taken by the Plane to Go from A to B
1. Calculating the Resultant Velocity:
- The resultant velocity in the direction of B can be calculated using the components:
Vyg=150sinα+20
Vxg=150cosα
- The magnitude of the resultant velocity (V_g) can be calculated using Pythagorean theorem:
Vg=√(Vxg)2+(Vyg)2
2. Calculating the Time:
- The distance from A to B is 500 km (which is 500,000 m).
- The time taken (t) can be calculated using:
t=DistanceVelocity=500,000mVg
3. Final Calculation:
- Substitute the values of V_g calculated from the components to find the time in seconds and convert it to minutes.
Final Answers:
- (a) The pilot should head the plane at an angle α, where α = sin^{-1}(1/15).
- (b) The time taken by the plane to go from A to B is approximately 50 minutes.
- The distance from point A to point B is 500 km at an angle of 30° east of north.
- The wind is blowing due north at a speed of 20 m/s.
- The airspeed of the plane is 150 m/s.
- Let’s define the north direction as the positive y-axis and the east direction as the positive x-axis.
- The angle of 30° east of north means that the direction from A to B can be represented in vector form.
- The velocity of the wind (V_wind) is purely in the y-direction:
Vwind=20m/s^j
- The velocity of the plane (V_plane) can be broken down into components based on the angle α (the angle the pilot should head):
Vplane=150m/s(cosα^i+sinα^j)
- The resultant velocity of the plane with respect to the ground (V_g) must point towards B:
Vg=Vplane+Vwind
- The x-component of V_g must be equal to the x-component of the direction to B, and the y-component must balance the wind.
- The angle to B gives us:
tan(30°)=VygVxg
- The y-component of V_g:
Vyg=150sinα+20
- The x-component of V_g:
Vxg=150cosα
- From the angle:
tan(30°)=1√3=150sinα+20150cosα
- Rearranging gives:
150sinα+20=150cosα√3
- Rearranging and substituting known values allows us to isolate and solve for sin(α) and cos(α).
- After calculations, we find:
sinα=115⟹α=sin−1(115)
- The resultant velocity in the direction of B can be calculated using the components:
Vyg=150sinα+20
Vxg=150cosα
- The magnitude of the resultant velocity (V_g) can be calculated using Pythagorean theorem:
Vg=√(Vxg)2+(Vyg)2
- The distance from A to B is 500 km (which is 500,000 m).
- The time taken (t) can be calculated using:
t=DistanceVelocity=500,000mVg
- Substitute the values of V_g calculated from the components to find the time in seconds and convert it to minutes.
- (a) The pilot should head the plane at an angle α, where α = sin^{-1}(1/15).
- (b) The time taken by the plane to go from A to B is approximately 50 minutes.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
An aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
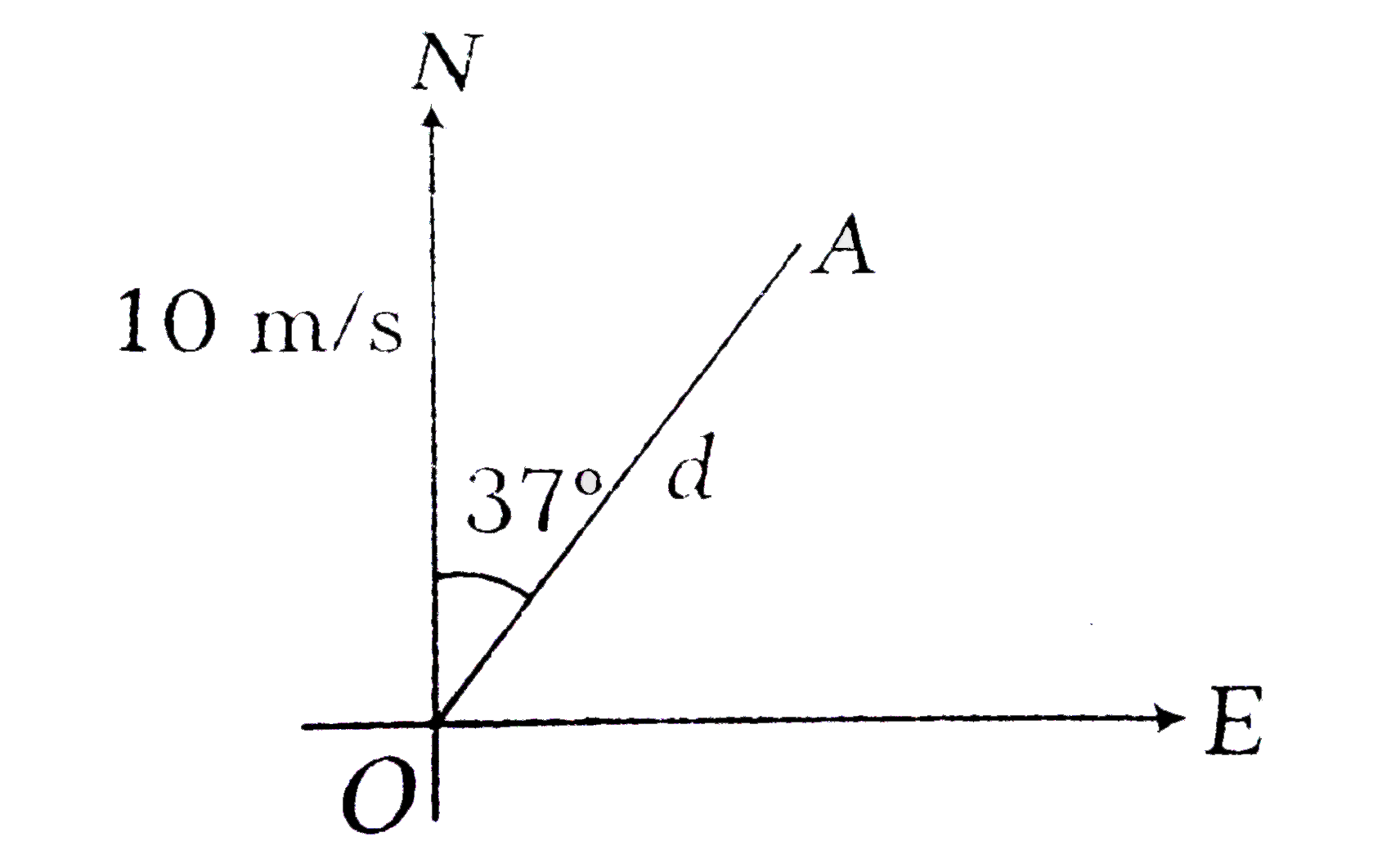
View Solution
Knowledge Check
A train of 150 m length is going towards north direction at a speed of 10 m/s. A bird flies at a speed of 5 m/s towards south direction parallel to the railway track. The time taken by the bird to cross the train is equal to
A20 secB16 secC12 secD10 sec
An aeroplane takes off from Mumbai to Delhi with velocity 50 kph at an angle 30∘ north of east. Wind is blowing at 25 kph from north to south. What is the resultant displacement of aeroplane in 2 hrs. (in km)
View SolutionRain is falling vertically with a speed of 30 m/s. wind starts blowing after some time with a speed of 15 m/s in east to west direction. In which direction should a boy waiting at a bus hold his umbrella ?
View SolutionA ship is travelling due east at a speed of 15km/h. Find the speed of a boat heading 30∘ east of north if it appears always due north from the ship.
View SolutionRam moves in east direction at a speed of 6 m/s and Shyam moves 30∘ east of north at a speed of 6 m/s. The magnitude of their relative velocity is
View SolutionThe wind is blowing due south with speed of 3m/sec. How fast should a car travel due east in order that the wind shall hasve a speed of 5m/sec relative to the car.
View SolutionA 210 meter long train is moving due north at a of 25 m/s. a small bird is flying due south a little above the train with speed 5 m/s. The time taken by the bird to cross the train is
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.
View Solution
