Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
The correct Answer is:A, B
To solve the problem of six particles situated at the corners of a regular hexagon of side length a moving at a constant speed v towards each other, we can break down the motion and calculate the time it takes for them to meet at the center. Here’s a step-by-step solution:
Step 1: Understanding the Setup
We have six particles located at the corners of a regular hexagon. Let's label the particles as A,B,C,D,E, and F. Each particle moves towards the next particle in a clockwise manner.
Step 2: Analyzing the Motion
When particle A moves towards particle B, it is not moving directly towards the center of the hexagon, but rather at an angle. The same applies to all other particles.
Step 3: Determine the Angle
In a regular hexagon, the angle subtended at the center by each side is 60∘. Therefore, the angle θ between the direction of motion of each particle and the line connecting the center of the hexagon to the particle is 30∘.
Step 4: Velocity Components
The velocity of each particle can be resolved into two components:
- The component towards the center of the hexagon, which is vcos(30∘).
- The component perpendicular to the line connecting the particles, which does not contribute to closing the distance between them.
Step 5: Calculate the Closing Speed
Since each particle is moving towards the next one, the effective closing speed between any two adjacent particles (say A and B) can be calculated as:
veffective=v−vcos(30∘)
Using cos(30∘)=√32, we find:
veffective=v−v⋅√32=v(1−√32)
Step 6: Calculate the Time to Meet
The initial distance between any two adjacent particles is a. The time t taken for the particles to meet can be calculated using the formula:
t=DistanceRelative Velocity=aveffective
Substituting the effective velocity:
t=av(1−√32)
Step 7: Simplifying the Expression
To simplify the expression, we can calculate 1−√32 and substitute it back into the equation. However, for practical purposes, we can keep it in this form.
Final Answer
Thus, the time taken for the particles to meet at the center of the hexagon is:
t=av(1−√32)
We have six particles located at the corners of a regular hexagon. Let's label the particles as A,B,C,D,E, and F. Each particle moves towards the next particle in a clockwise manner.
When particle A moves towards particle B, it is not moving directly towards the center of the hexagon, but rather at an angle. The same applies to all other particles.
In a regular hexagon, the angle subtended at the center by each side is 60∘. Therefore, the angle θ between the direction of motion of each particle and the line connecting the center of the hexagon to the particle is 30∘.
The velocity of each particle can be resolved into two components:
- The component towards the center of the hexagon, which is vcos(30∘).
- The component perpendicular to the line connecting the particles, which does not contribute to closing the distance between them.
Since each particle is moving towards the next one, the effective closing speed between any two adjacent particles (say A and B) can be calculated as:
veffective=v−vcos(30∘)
Using cos(30∘)=√32, we find:
veffective=v−v⋅√32=v(1−√32)
The initial distance between any two adjacent particles is a. The time t taken for the particles to meet can be calculated using the formula:
t=DistanceRelative Velocity=aveffective
Substituting the effective velocity:
t=av(1−√32)
To simplify the expression, we can calculate 1−√32 and substitute it back into the equation. However, for practical purposes, we can keep it in this form.
Thus, the time taken for the particles to meet at the center of the hexagon is:
t=av(1−√32)
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
Three particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant

View Solutionsix particles are situated at the corners of a regular hexagon. These particles start moving with equal speed of 10 m/s in such that velocity of any one particle is directed towards the next particle. Find the rate (in m/s) at which length of a side of the hexagon is decreasing.
View SolutionFour particles A,B,CandD are situated at the corner of a square ABCD of side a at t-0. Each of particles moves with constant speed (v). A always has its velocity along AB,B along BC,C along CD~andD along DA. At what time will these particles meet each other ?
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionSeven particles are placed at the seven corners of a cube of side 'a' (except at origin ) . The mass of each particle is 'm' . The centre of mass of the system is
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View Solutionn' number of particles are located at the verticles of a regular polygon of n sides having the edge length 'a'. They all start moving simultaneously with equal constant speed 'v' heading towards each other all the time. How long will the particles take to collide?
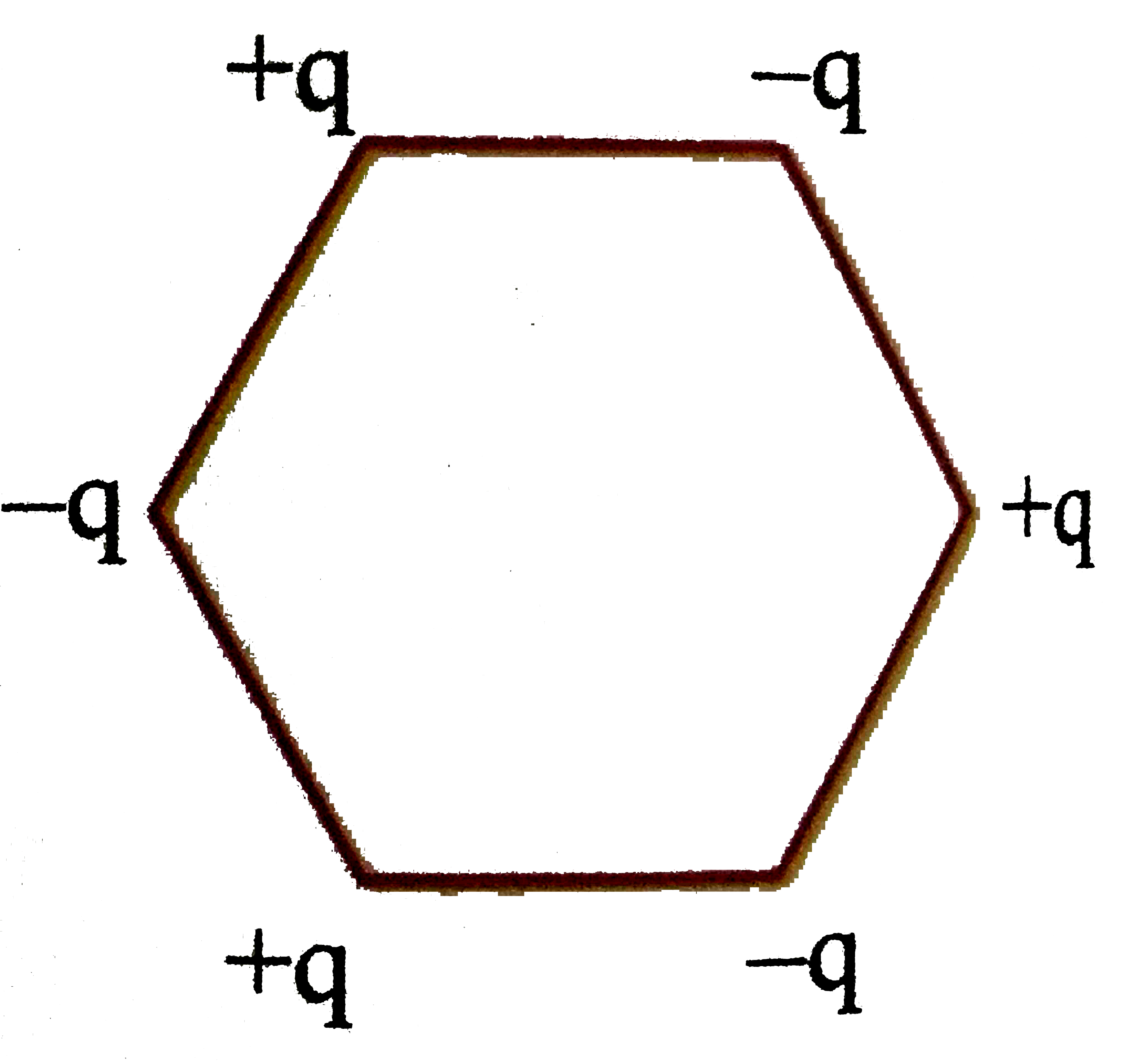
View SolutionSix charge of magnitude +q and −q are fixed at the corners of a regular hexagon of edge length a as shown in the figure .The electrostatic interaction energy of the charged particle is :
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
In the above system, if two particles are kept fixed and third particle is released, then speed of the particle when it reaches to the mid point of the side connectiong other two masses is
View Solution
