Find the ratio of the magnitude of the electric force to the grativational force acting between two protons.
The correct Answer is:A, B, C, D
To find the ratio of the magnitude of the electric force to the gravitational force acting between two protons, we can follow these steps:
Step 1: Identify the Constants
- The charge of a proton q is 1.6×10−19 coulombs.
- The mass of a proton m is 1.67×10−27 kg.
- The gravitational constant G is 6.67×10−11N m2/kg2.
- The permittivity of free space ϵ0 is 8.85×10−12C2/N m2.
Step 2: Calculate the Electric Force
The electric force Fe between two charges is given by Coulomb's law:
Fe=14πϵ0⋅q1⋅q2r2
Since both charges are protons, we can substitute q1=q2=q:
Fe=14πϵ0⋅q2r2
Substituting the values:
Fe=9×109⋅(1.6×10−19)2r2
Step 3: Calculate the Gravitational Force
The gravitational force Fg between two masses is given by Newton's law of gravitation:
Fg=G⋅m1⋅m2r2
Since both masses are protons, we can substitute m1=m2=m:
Fg=G⋅m2r2
Substituting the values:
Fg=6.67×10−11⋅(1.67×10−27)2r2
Step 4: Calculate the Ratio of Electric Force to Gravitational Force
Now, we can find the ratio FeFg:
FeFg=9×109⋅(1.6×10−19)2r26.67×10−11⋅(1.67×10−27)2r2
The r2 cancels out:
FeFg=9×109⋅(1.6×10−19)26.67×10−11⋅(1.67×10−27)2
Step 5: Substitute the Values and Simplify
Now, substituting the values:
FeFg=9×109⋅(2.56×10−38)6.67×10−11⋅(2.7889×10−54)
Calculating the numerator:
9×109⋅2.56×10−38=2.304×10−28
Calculating the denominator:
6.67×10−11⋅2.7889×10−54=1.857×10−64
Now, dividing the two results:
FeFg=2.304×10−281.857×10−64≈1.24×1036
Final Answer
The ratio of the magnitude of the electric force to the gravitational force acting between two protons is approximately:
FeFg≈1.24×1036
---
- The charge of a proton q is 1.6×10−19 coulombs.
- The mass of a proton m is 1.67×10−27 kg.
- The gravitational constant G is 6.67×10−11N m2/kg2.
- The permittivity of free space ϵ0 is 8.85×10−12C2/N m2.
The electric force Fe between two charges is given by Coulomb's law:
Fe=14πϵ0⋅q1⋅q2r2
Since both charges are protons, we can substitute q1=q2=q:
Fe=14πϵ0⋅q2r2
Substituting the values:
Fe=9×109⋅(1.6×10−19)2r2
The gravitational force Fg between two masses is given by Newton's law of gravitation:
Fg=G⋅m1⋅m2r2
Since both masses are protons, we can substitute m1=m2=m:
Fg=G⋅m2r2
Substituting the values:
Fg=6.67×10−11⋅(1.67×10−27)2r2
Now, we can find the ratio FeFg:
FeFg=9×109⋅(1.6×10−19)2r26.67×10−11⋅(1.67×10−27)2r2
The r2 cancels out:
FeFg=9×109⋅(1.6×10−19)26.67×10−11⋅(1.67×10−27)2
Now, substituting the values:
FeFg=9×109⋅(2.56×10−38)6.67×10−11⋅(2.7889×10−54)
Calculating the numerator:
9×109⋅2.56×10−38=2.304×10−28
Calculating the denominator:
6.67×10−11⋅2.7889×10−54=1.857×10−64
Now, dividing the two results:
FeFg=2.304×10−281.857×10−64≈1.24×1036
The ratio of the magnitude of the electric force to the gravitational force acting between two protons is approximately:
FeFg≈1.24×1036
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Objective -27videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - All Questions75videos
SPECIFIC HEAT CAPACITIES OF GASES
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of magnitude of electrostatic force and gravitational force for an electron and a proton is
A6.6×1039B2.4×1039C6.6×1029D2.4×1029
Calculate the ratio of electric to gravitational force between two electrons.
View SolutionWith increase of temperature, the frictional force acting between two surfaces
View SolutionFind the magnitude of the resultant of shown forces :-
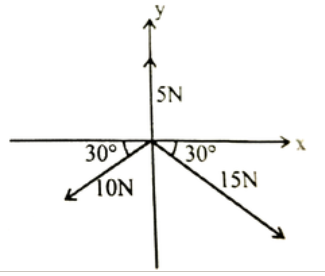 View Solution
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?View SolutionTwo forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
View SolutionTwo forces F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is
View SolutionTwo force F1 and F2 are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-
View Solution

