Two blocks A and B of mass mAandmB respectively are kept in contact on a frictionless table. The experimenter pushes the block A from behind so that the blocks accelerate. If the block A exerts a fore F on the block B, what is the force exerted by the experimenter on A?
To solve the problem, we will follow these steps:
Step 1: Identify the forces acting on the blocks
We have two blocks A and B with masses mA and mB respectively. The experimenter applies a force F′ on block A. Block A exerts a force F on block B.
Step 2: Write the equation of motion for the system
Since both blocks are in contact and on a frictionless surface, they will accelerate together. The total mass of the system is mA+mB. The net force acting on the system is F′, which causes the acceleration a.
Using Newton's second law:
F′=(mA+mB)a
Step 3: Express acceleration in terms of the applied force
From the equation above, we can express the acceleration a as:
a=F′mA+mB
Step 4: Analyze block B
Block B experiences a force F exerted by block A. According to Newton's second law for block B:
F=mB⋅a
Step 5: Substitute the expression for acceleration into block B's equation
Substituting a from Step 3 into the equation for block B:
F=mB⋅F′mA+mB
Step 6: Solve for the force exerted by the experimenter on block A
Rearranging the equation from Step 5 gives us:
F′=F(mA+mB)mB
Step 7: Final expression for the force exerted by the experimenter
Thus, the force exerted by the experimenter on block A is:
F′=F(1+mAmB)
Summary
The force exerted by the experimenter on block A is given by:
F′=F(1+mAmB)
We have two blocks A and B with masses mA and mB respectively. The experimenter applies a force F′ on block A. Block A exerts a force F on block B.
Since both blocks are in contact and on a frictionless surface, they will accelerate together. The total mass of the system is mA+mB. The net force acting on the system is F′, which causes the acceleration a.
F′=(mA+mB)a
From the equation above, we can express the acceleration a as:
a=F′mA+mB
Block B experiences a force F exerted by block A. According to Newton's second law for block B:
F=mB⋅a
Substituting a from Step 3 into the equation for block B:
F=mB⋅F′mA+mB
Rearranging the equation from Step 5 gives us:
F′=F(mA+mB)mB
Thus, the force exerted by the experimenter on block A is:
F′=F(1+mAmB)
The force exerted by the experimenter on block A is given by:
F′=F(1+mAmB)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
Three blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.

View SolutionThree blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.

View SolutionBlocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
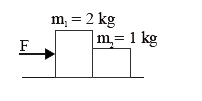
View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

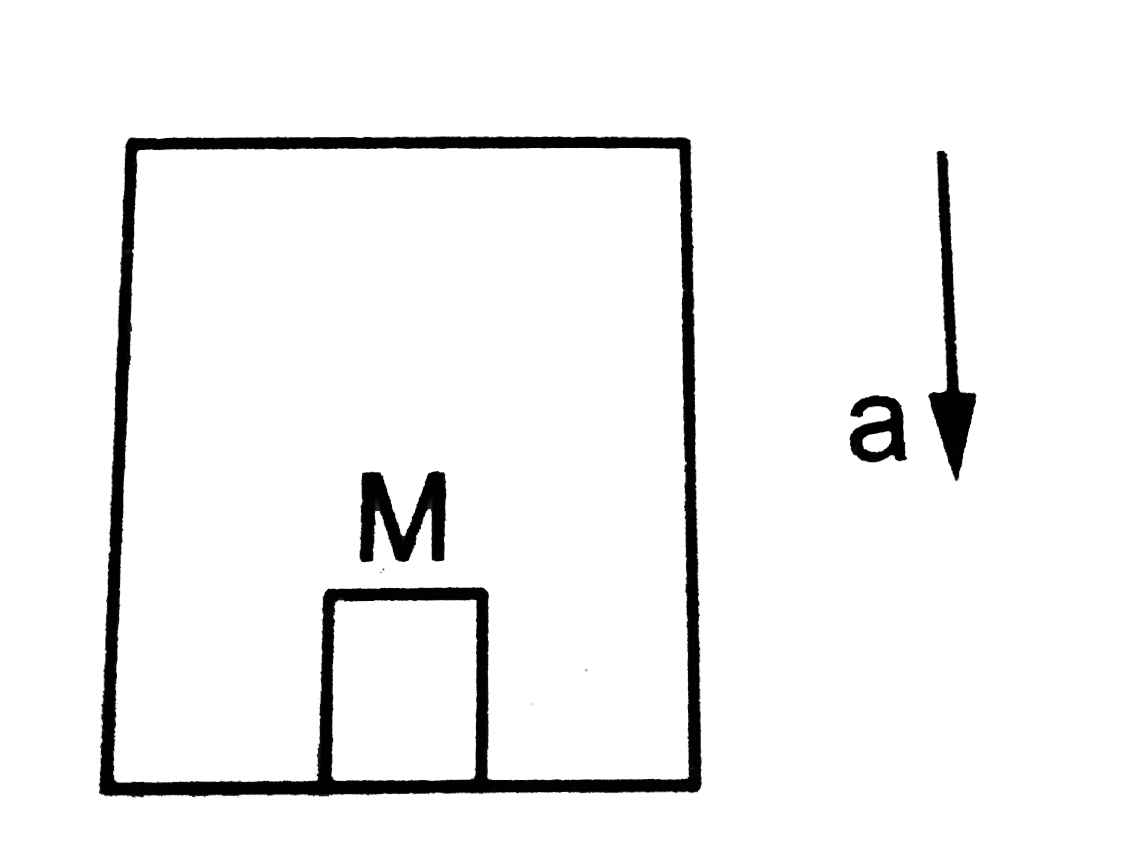
View SolutionWith what acceleration a should the box of figure descends so that the block of mass M exerts a force Mg/4 on the floor of the box?
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo blocks of masses 5 kg and 2 kg are kept in contact with each other on a frictionless horizontal surface. If a force of 14 N is applied on the larger block what is the acceleration of the system ? What is the contact force between the two blocks ?
View Solution
