Two identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
To find the work done by gravity in equalizing the levels of the liquid in two identical cylindrical vessels when they are connected, we can follow these steps:
Step 1: Understand the Initial Conditions
We have two identical cylindrical vessels with:
- Density of the liquid: ρ
- Height of the liquid in the first vessel: h1
- Height of the liquid in the second vessel: h2
- Area of the base of each vessel: A
Step 2: Determine the Final Height
When the two vessels are connected, the liquid will equalize to a common height. The average height of the liquid after equalization can be calculated as:
hf=h1+h22
Step 3: Calculate the Change in Height
For the first vessel, the change in height (decrease) is:
Δh1=h1−hf=h1−h1+h22=h1−h22
For the second vessel, the change in height (increase) is:
Δh2=hf−h2=h1+h22−h2=h1−h22
Step 4: Calculate the Volume of Liquid Moved
The volume of the liquid that moves from the first vessel is:
V1=A⋅Δh1=A⋅h1−h22
The volume of the liquid that moves into the second vessel is:
V2=A⋅Δh2=A⋅h1−h22
Step 5: Calculate the Mass of the Liquid Moved
The mass of the liquid moved from the first vessel is:
m1=ρ⋅V1=ρ⋅A⋅h1−h22
The mass of the liquid moved into the second vessel is:
m2=ρ⋅V2=ρ⋅A⋅h1−h22
Step 6: Calculate the Work Done by Gravity
The work done by gravity when the liquid moves down by Δh1 in the first vessel is:
W1=m1⋅g⋅Δh1=(ρ⋅A⋅h1−h22)⋅g⋅h1−h22
The work done by gravity when the liquid moves up by Δh2 in the second vessel is:
W2=m2⋅g⋅Δh2=(ρ⋅A⋅h1−h22)⋅g⋅h1−h22
Since W1 is negative (work done against gravity) and W2 is positive (work done by gravity), the total work done W is:
W=W1+W2=−ρAg(h1−h2)24
Final Answer
The work done by gravity in equalizing the levels is:
W=ρAg(h1−h2)24
We have two identical cylindrical vessels with:
- Density of the liquid: ρ
- Height of the liquid in the first vessel: h1
- Height of the liquid in the second vessel: h2
- Area of the base of each vessel: A
When the two vessels are connected, the liquid will equalize to a common height. The average height of the liquid after equalization can be calculated as:
hf=h1+h22
For the first vessel, the change in height (decrease) is:
Δh1=h1−hf=h1−h1+h22=h1−h22
For the second vessel, the change in height (increase) is:
Δh2=hf−h2=h1+h22−h2=h1−h22
The volume of the liquid that moves from the first vessel is:
V1=A⋅Δh1=A⋅h1−h22
The volume of the liquid that moves into the second vessel is:
V2=A⋅Δh2=A⋅h1−h22
The mass of the liquid moved from the first vessel is:
m1=ρ⋅V1=ρ⋅A⋅h1−h22
The mass of the liquid moved into the second vessel is:
m2=ρ⋅V2=ρ⋅A⋅h1−h22
The work done by gravity when the liquid moves down by Δh1 in the first vessel is:
W1=m1⋅g⋅Δh1=(ρ⋅A⋅h1−h22)⋅g⋅h1−h22
The work done by gravity when the liquid moves up by Δh2 in the second vessel is:
W2=m2⋅g⋅Δh2=(ρ⋅A⋅h1−h22)⋅g⋅h1−h22
W=W1+W2=−ρAg(h1−h2)24
The work done by gravity in equalizing the levels is:
W=ρAg(h1−h2)24
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -1
10 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -2
8 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
Two identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionA U-tube of cross section A and 2A contains liquid of density ρ. Initially, the liquid in the two arms are held with a level difference h as shown in figure. After being released the levels equalize after some time. The work done by gravity forces on the liquid in the process is :
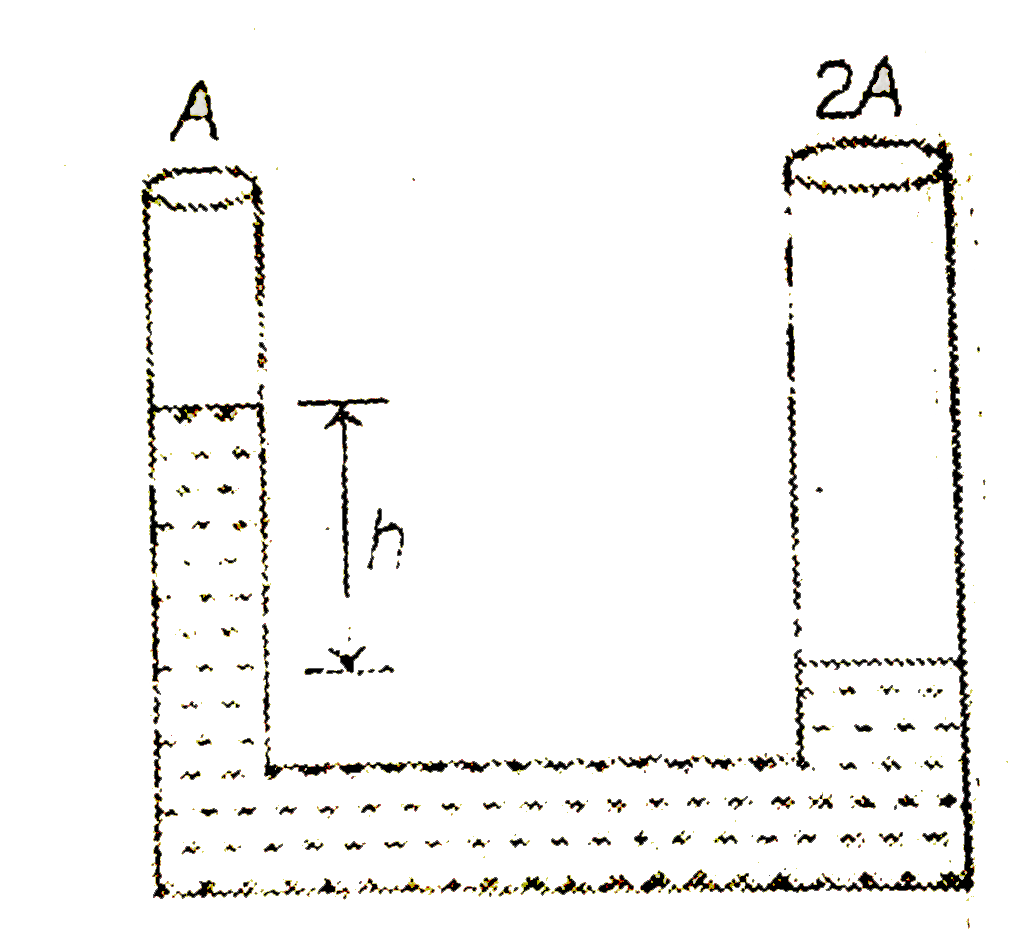
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View Solution_E01_040_Q01.png)
Two vessels A and B have the same base area and contain water to the same height but the mass of water in A is four times that in B. The ratio of the liquid thrust at the base of A to that at the base of B is
View SolutionA cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the ratio of magnitude of torque on one side wall to the torque on base about the same axis
View SolutionIn a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

View Solution
