A heavy particle is suspended by a stirng of length l. The particle is given a horizontal velocity $v_{0}$ . The stirng becomes slack at some angle and the particle proceeds on a parabola.find the value of $v_{0}$ if the prticle psses through the ponit of suspension

Video Solution

Text Solution

Verified by Experts

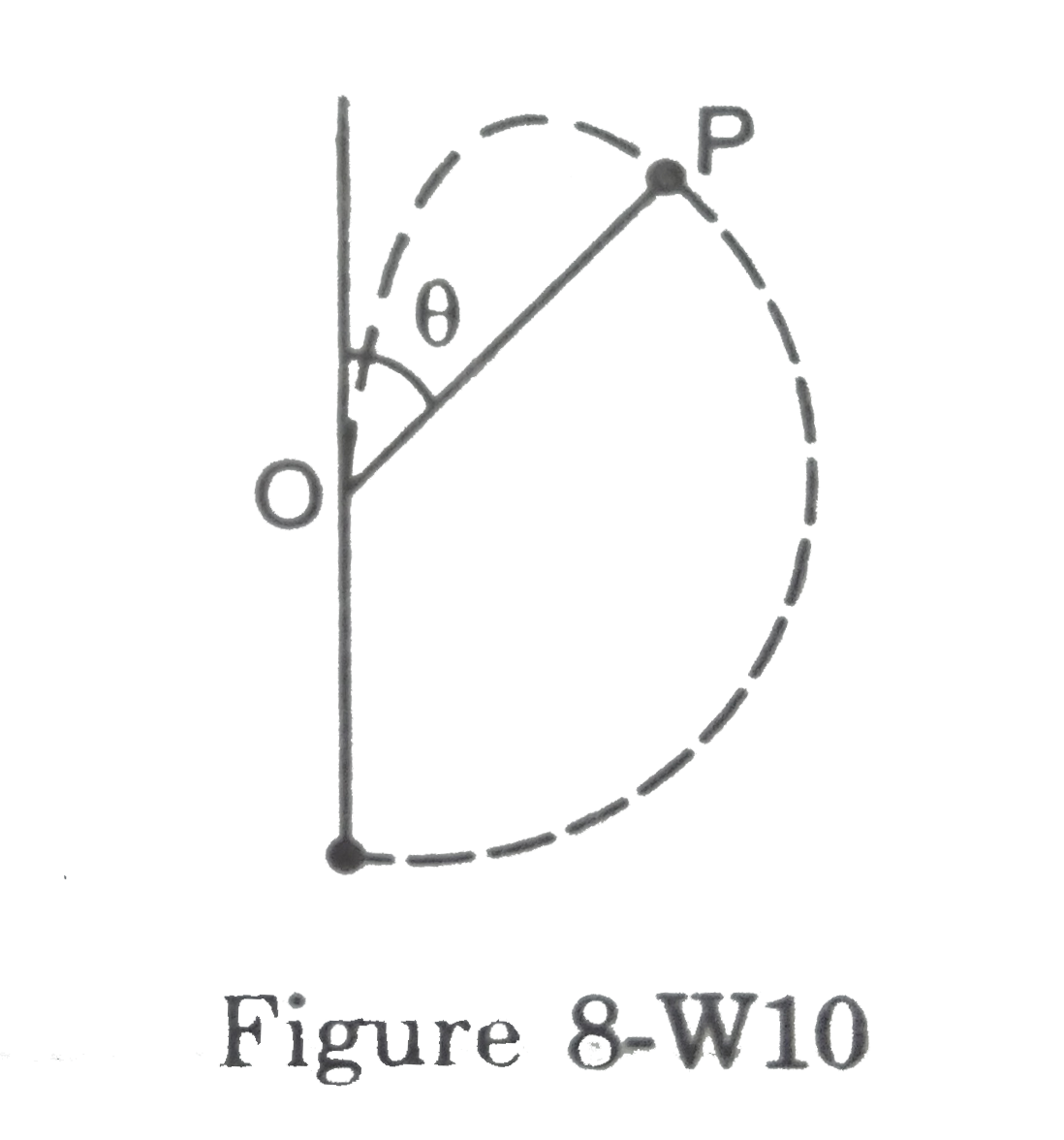
Suppose the string becomes slack when the particle reaches the point P ure. Suppose the string OP makes an angle $θ$ with the upward vertical. The only force actig on the particle at P is its weight mg.The radia component of the force is $m g cos θ$ . As the particle moves on the circle upto P,
$m g cos θ = m (\frac{v^{2}}{l})$
or, $v^{2} = g l cos θ$ ...........i
where v is its speed at P. Using conservation of energy,
$\frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v^{2} + m g l (1 + cos θ)$
or $v^{2} = v^{2}_0 - 2 g l (1 + cos θ)$ ......ii
From i and ii $v_{0}^{2} - 2 g l (1 + cos θ) = g l cos θ$
or, $v_{0}^{2} = g l (2 + 3 cos θ)$ .........iii
Now onwards the particle goes in a parabola under the action of gravity. As it passes through the point of suspension O, the equations for horizontal and verticla motions give,
$l sin θ = (v cos θ) t$
and $- l cos θ = (v cos θ) t - \frac{1}{2} >^{2}$
or, $- l cos θ = (v sin θ (\frac{l sin θ}{v cos θ}) - \frac{1}{2} {g (\frac{l sin θ}{v cos θ})}^{2}$
or $- {cos}^{2} θ = {sin}^{2} θ - \frac{1}{2} \frac{g (l {sin}^{2} θ)}{v^{2} cos θ}$
or $- {cos}^{2} t h e t = 1 - {cos}^{2} t h e a t a - \frac{1}{2} \frac{g l {sin}^{2} θ}{2 g l {cos}^{2} θ} [o m i]$
or, $= \frac{1}{2} {tan}^{2} θ$
$or tan θ = \sqrt{2}$
From iii $v_{0} = {[g l (2 + \sqrt{3})]}^{\frac{1}{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

HC VERMA ENGLISH-WORK AND ENERGY-Worked out Examples

Home
Ask Doubt
Profile