Two bodies make an elastic head on colision on a smooth horizontal table kept in a car.Do you expect a change in the result if the car is accelerated on a horizontal road because of the noninertial character of the frame? Does the equation velocityof separation = velocity of approach remain valid in n accelerating car? Does the equation final momentum =initial momentum remain valid in the accelerating car?
To solve the question regarding the elastic head-on collision of two bodies on a smooth horizontal table kept in an accelerating car, we will analyze the situation step by step.
Step 1: Understanding Elastic Collisions
In an elastic collision, two key principles hold true:
1. Conservation of Momentum: The total momentum before the collision equals the total momentum after the collision.
2. Velocity of Separation = Velocity of Approach: The relative velocity of separation of the two bodies after the collision is equal to the relative velocity of approach before the collision.
Step 2: Non-Inertial Frame of Reference
When the car is accelerating, it creates a non-inertial frame of reference. In such a frame, an additional pseudo force acts on the bodies due to the acceleration of the car. This pseudo force alters the dynamics of the collision.
Step 3: Effect of Pseudo Force
The presence of the pseudo force means that the system (the two bodies on the table) is no longer isolated. The pseudo force acts in the opposite direction of the car's acceleration, affecting the motion of the bodies during the collision.
Step 4: Validity of Conservation Equations
1. Velocity of Separation = Velocity of Approach: This equation will not hold true in the accelerating car because the pseudo force influences the velocities of the bodies during the collision.
2. Final Momentum = Initial Momentum: This equation also does not hold true in the accelerating car due to the external pseudo force acting on the system.
Conclusion
In conclusion, when the car is accelerating, both the equations of conservation of momentum and the relationship between the velocities of separation and approach do not remain valid. Therefore, we expect a change in the results of the collision compared to when the car is at rest or moving with uniform velocity.
---
In an elastic collision, two key principles hold true:
1. Conservation of Momentum: The total momentum before the collision equals the total momentum after the collision.
2. Velocity of Separation = Velocity of Approach: The relative velocity of separation of the two bodies after the collision is equal to the relative velocity of approach before the collision.
When the car is accelerating, it creates a non-inertial frame of reference. In such a frame, an additional pseudo force acts on the bodies due to the acceleration of the car. This pseudo force alters the dynamics of the collision.
The presence of the pseudo force means that the system (the two bodies on the table) is no longer isolated. The pseudo force acts in the opposite direction of the car's acceleration, affecting the motion of the bodies during the collision.
1. Velocity of Separation = Velocity of Approach: This equation will not hold true in the accelerating car because the pseudo force influences the velocities of the bodies during the collision.
2. Final Momentum = Initial Momentum: This equation also does not hold true in the accelerating car due to the external pseudo force acting on the system.
In conclusion, when the car is accelerating, both the equations of conservation of momentum and the relationship between the velocities of separation and approach do not remain valid. Therefore, we expect a change in the results of the collision compared to when the car is at rest or moving with uniform velocity.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A collision experiment is done on a horizontal table kept in an elevator. Do you expect a change in the results if the elevator is accelerated up or down because of the noninertial character of the frame?
View SolutionA car weighing 1600 kg moving with a velocity of 30 m/s retards uniformly coming to rest in 2 seconds . Calculate the
(i) Initial and final momentum of the car
(ii) Rate of change of momentum of the car .
(iii) Acceleration of the car .
View SolutionA bob suspended from the ceiling of a car which is accelerating on a horizontal road. The bob stays t rest with respect to the car when the string is making an angle θ with the vertical.The linear momentum of the bob as seen from the road is increasing with momentum? If not, where is the external force which changes the linear momentum?
View SolutionTwo cars A and B of equal masses (100Kg) are moving on a straight horizontal road with same velocity 3m/s as shown. At t=0 car A starts accelerating with constant acceleration of 2m/s2 (intial separation between car is 25m). Choose correct options (neglect length of cars)

View SolutionSTATEMENT-1 : Two bodies of mass M and 2M released from rest and they move towards each other due to their mutual gravitational force of attraction and collide at mid point.
STATEMENT-2 : If the total mechanical energy of a body is zero than its linear momentum is necessarily non zero at any point other than reference point.
STATEMENT-3 : The linear momentum of the bob of a simple pendulum suspended by the roof of a car accelerating on a horizontal road increases due to tension in the string of the pendulum.
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
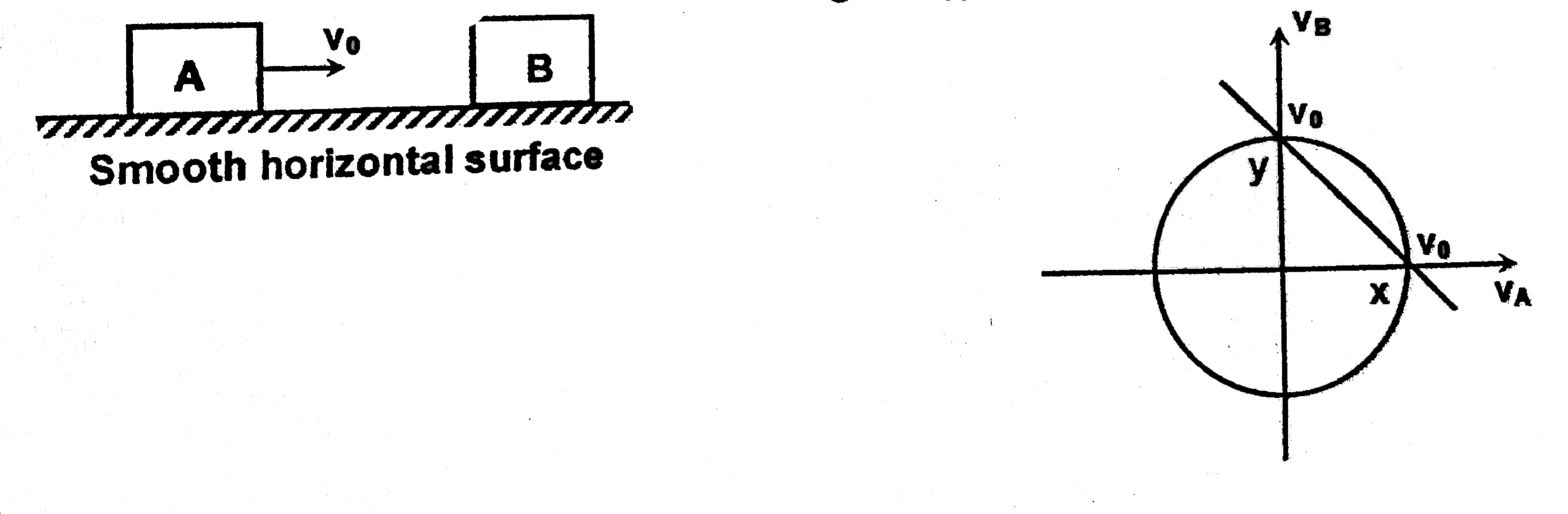
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
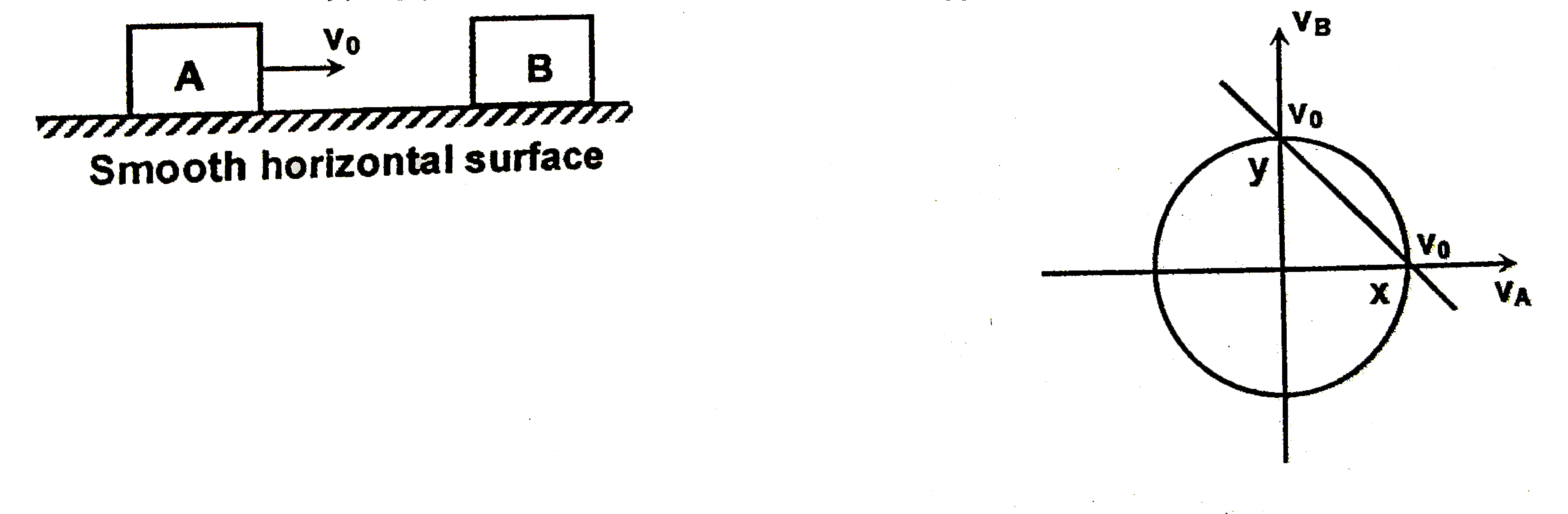
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot is
View Solution
