A block of mass 180g is suspended by a massless spring. The spring extends by 1.8cm due to the weight of block. A particle of mass 20g is dropped from a height 80cm on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the spring constant (k)
Given:
- Mass of the block (m) = 180 g = 0.18 kg
- Extension of the spring (x) = 1.8 cm = 0.018 m
- Acceleration due to gravity (g) = 9.8 m/s²
Using Hooke's Law:
kx=mg
k=mgx
Substituting the values:
k=0.18×9.80.018
k=1.7640.018
k=98N/m
Step 2: Calculate the velocity of the dropped particle just before collision
Given:
- Height (h) = 80 cm = 0.8 m
Using the equation of motion:
v2=u2+2gh
Since the initial velocity (u) is 0:
v2=0+2×9.8×0.8
v2=15.68
v=√15.68
v≈3.96m/s
Step 3: Calculate the final velocity after the inelastic collision
Given:
- Mass of the dropped particle (m1) = 20 g = 0.02 kg
- Mass of the block (m2) = 180 g = 0.18 kg
Using conservation of momentum:
m1v1+m2v2=(m1+m2)vf
Where v2=0 (block is at rest before collision):
0.02×3.96+0.18×0=(0.02+0.18)vf
0.0792=0.20vf
vf=0.07920.20
vf=0.396m/s
Step 4: Calculate the maximum elongation of the spring
At maximum elongation, the kinetic energy will convert into potential energy stored in the spring and the work done against gravity.
Using the conservation of energy:
12(m1+m2)v2f+(m1+m2)gh=12k(x2f−x20)
Where:
- h is the additional elongation of the spring,
- xf is the total elongation,
- x0 is the initial elongation (1.8 cm = 0.018 m).
Rearranging gives:
12(0.20)(0.396)2+(0.20)(9.8)(h)=12(100)(x2f−(0.018)2)
Calculating the left side:
12(0.20)(0.156816)+(0.20)(9.8)(h)=0.0156816+1.96h
Calculating the right side:
50(x2f−0.000324)
Setting both sides equal:
0.0156816+1.96h=50x2f−0.0162
Step 5: Solve for maximum elongation
Assuming maximum elongation occurs when the spring is fully extended, we can simplify the equation. Let xf=x0+h:
0.0156816+1.96h=50((0.018+h)2−0.000324)
This will lead to a quadratic equation in terms of h. Solving this will give us the maximum elongation.
Final Result
After solving the quadratic equation, we find:
- The total maximum elongation xf=3.8cm.
Given:
- Mass of the block (m) = 180 g = 0.18 kg
- Extension of the spring (x) = 1.8 cm = 0.018 m
- Acceleration due to gravity (g) = 9.8 m/s²
kx=mg
k=mgx
k=0.18×9.80.018
k=1.7640.018
k=98N/m
Given:
- Height (h) = 80 cm = 0.8 m
v2=u2+2gh
Since the initial velocity (u) is 0:
v2=0+2×9.8×0.8
v2=15.68
v=√15.68
v≈3.96m/s
Given:
- Mass of the dropped particle (m1) = 20 g = 0.02 kg
- Mass of the block (m2) = 180 g = 0.18 kg
m1v1+m2v2=(m1+m2)vf
Where v2=0 (block is at rest before collision):
0.02×3.96+0.18×0=(0.02+0.18)vf
0.0792=0.20vf
vf=0.07920.20
vf=0.396m/s
At maximum elongation, the kinetic energy will convert into potential energy stored in the spring and the work done against gravity.
12(m1+m2)v2f+(m1+m2)gh=12k(x2f−x20)
- h is the additional elongation of the spring,
- xf is the total elongation,
- x0 is the initial elongation (1.8 cm = 0.018 m).
12(0.20)(0.396)2+(0.20)(9.8)(h)=12(100)(x2f−(0.018)2)
12(0.20)(0.156816)+(0.20)(9.8)(h)=0.0156816+1.96h
50(x2f−0.000324)
0.0156816+1.96h=50x2f−0.0162
Assuming maximum elongation occurs when the spring is fully extended, we can simplify the equation. Let xf=x0+h:
0.0156816+1.96h=50((0.018+h)2−0.000324)
After solving the quadratic equation, we find:
- The total maximum elongation xf=3.8cm.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Knowledge Check
A block of mass 2kg is propped from a heught of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5 cmB15 cmC20 cmD10 cm
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionAt t=0, a constant force is applied on 3kg block. Find out maximum elongation in spring in cm.
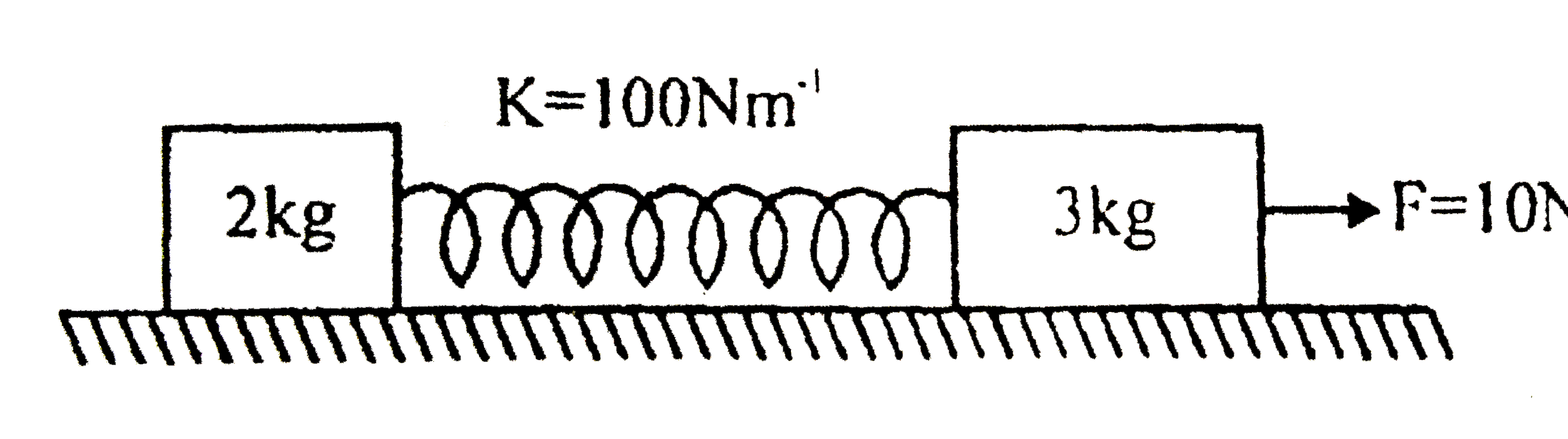
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring

View SolutionA block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View SolutionA block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View Solution

