The blocks shown in figure have equal masses. The surface of A is smooth but that of B has a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B if a. the collision is perfectly elastic and b. the collision is perfectly inelastic. Take g=10ms2.

V1=10ms
V2=0
v1,v2→ velcity of A and B after collision a. if the collision is perfectly elastic
mV1+mV2=Mv1+mv2
→10+0=v1+v2
v1+v2=10…..i
Again v1+v2=−(u1−v2)
=−(10.0)=−10…ii
Substracting ii frm ii
2v2=20
→v2=10ms
the deceleration of B
pu∈gworke≠rgypr∈cip≤<br>:.(1/2)xxmxx(0)^2-91/2)xxmxxv^2<br>=-mxxaxxh<br>rarr -(1/2)xx (10)^2=-mugxxh
→h=1002×1×10=50m
b. if the collision is perfectly in elastic
m×u1+m×u2=(m+m)×v
→m×10+m×0=2m×v
→v=(102)=5ms
The two blocks will move together sticking to each other
∴Pu∈gworke≠rgypr∈cip≤<br>(1/2)xx2mxx(0)^2xx2mxx(v)^2<br>=2mxxmugxxs<br>rarr ((5)^2)/(0.1xx10xx2)=S<br>=S=12.5m
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer25videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -118videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer9videos
CALORIMETRY
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
Similar Questions
The friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).
 View Solution
View SolutionA system is shown in the figure. Block A is moving with 1m/s towards left. Wedge is moving with 1m/s towards right. Then speed of the block B will be :
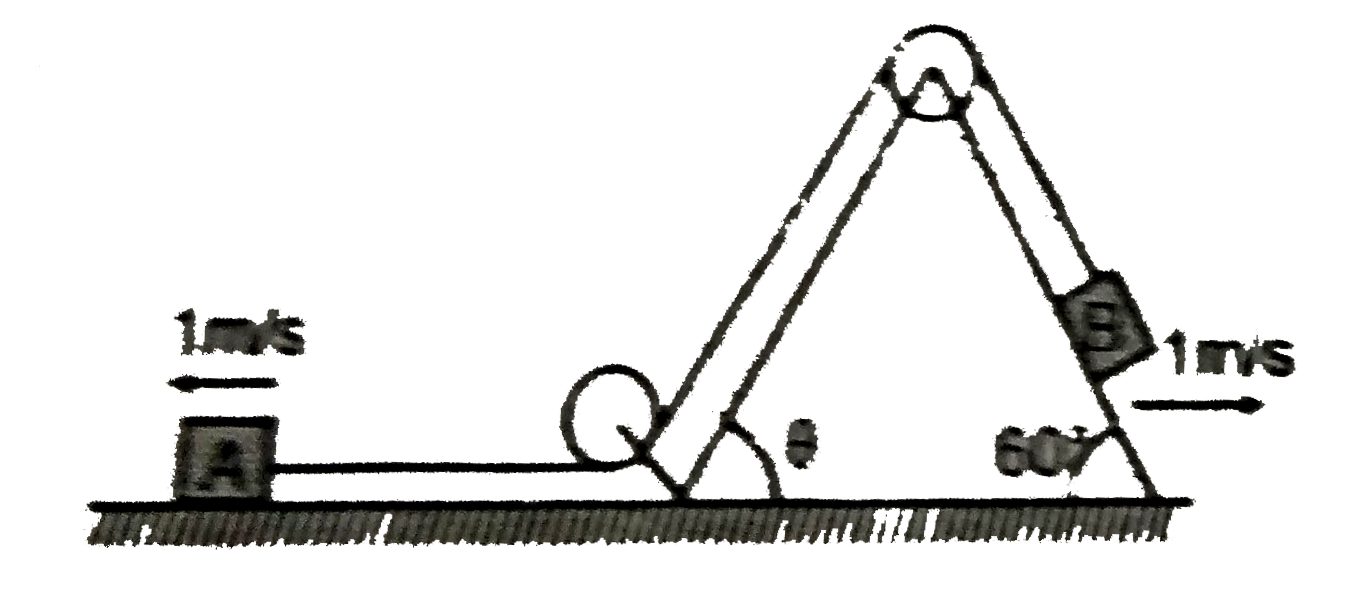 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two objects, one of mass 3 kg and moving with speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the object after the collision.
A0.25m/sB0.5m/sC0.75m/sD1m/s
Blocks shown in figure moves with constant velocity 10 m/s towards right. All surgaces in contact are rough. The friction force applied by B on A is :-
View SolutionTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
View SolutionThe friction coefficient between the horizontal surfce and ech of the blocks shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g=10ms2.
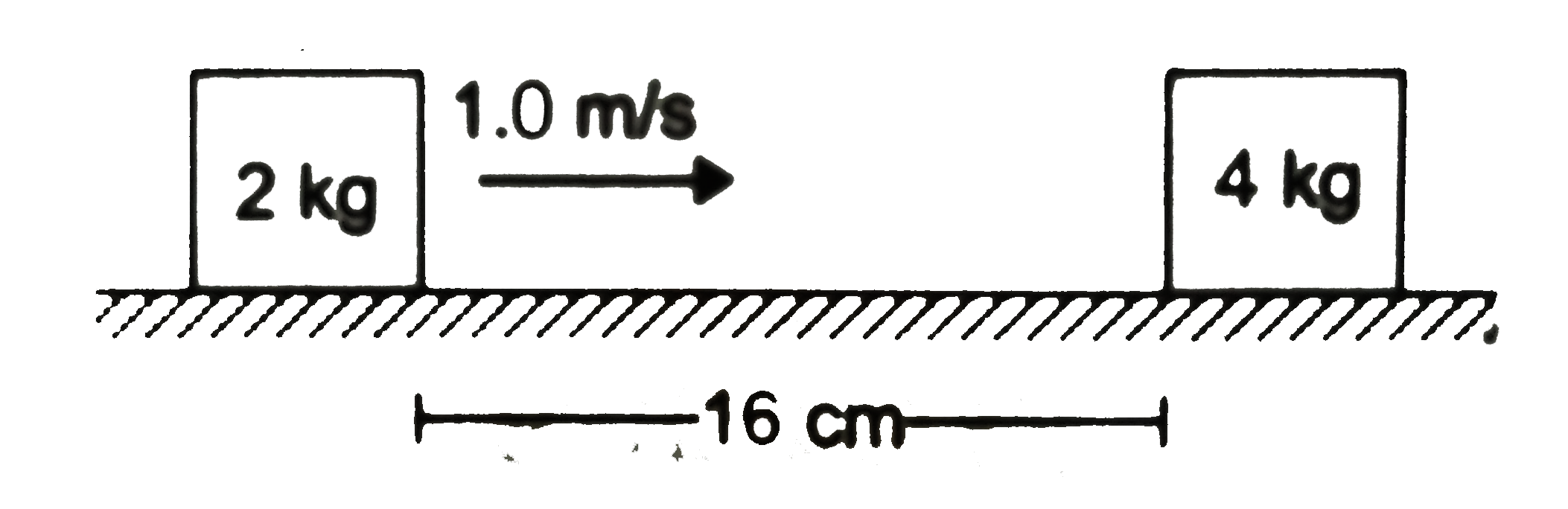 View Solution
View SolutionA buttle weighting 10 g and moving with a velocity 800ms−1 strikes a 10 kg block resting on a frictionless surface. The speed of the block after the perfectly inelastic collision is approximately
View SolutionThree blocks A, B and C are lying on a smooth horizontal surface, as shown in the figure. A and B have equal masses, m while C has mass M. Block A is given an inita speed v towards B due to which it collides with B perfectly inelastically. The combined mass collides with C, also perfectly inelastically 56th of the initial kinetic energy is lost in whole process. What is balue of M/m?
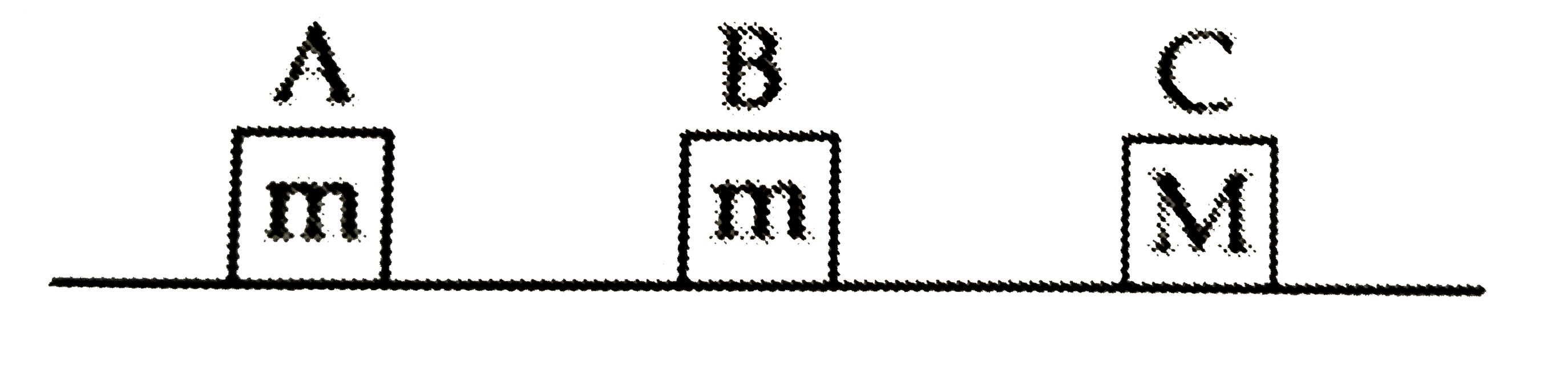 View Solution
View SolutionThe friction coefficient between the horizontal surface and blocks A and B are 115 and 215 respectively. The collision between the blocks is perfectly elastic. Find the separation (in meters) between the two blcoks when they come to rest.
View SolutionTwo particles of mass 1 kg and 2 kg are moving with speed 2 m/s and 5 m/s as shown in the figure, they collides perfectly inelastically. And second particle come to rest after collision. Find
(a) Their final velocity
(b) Loss in kinetic energy
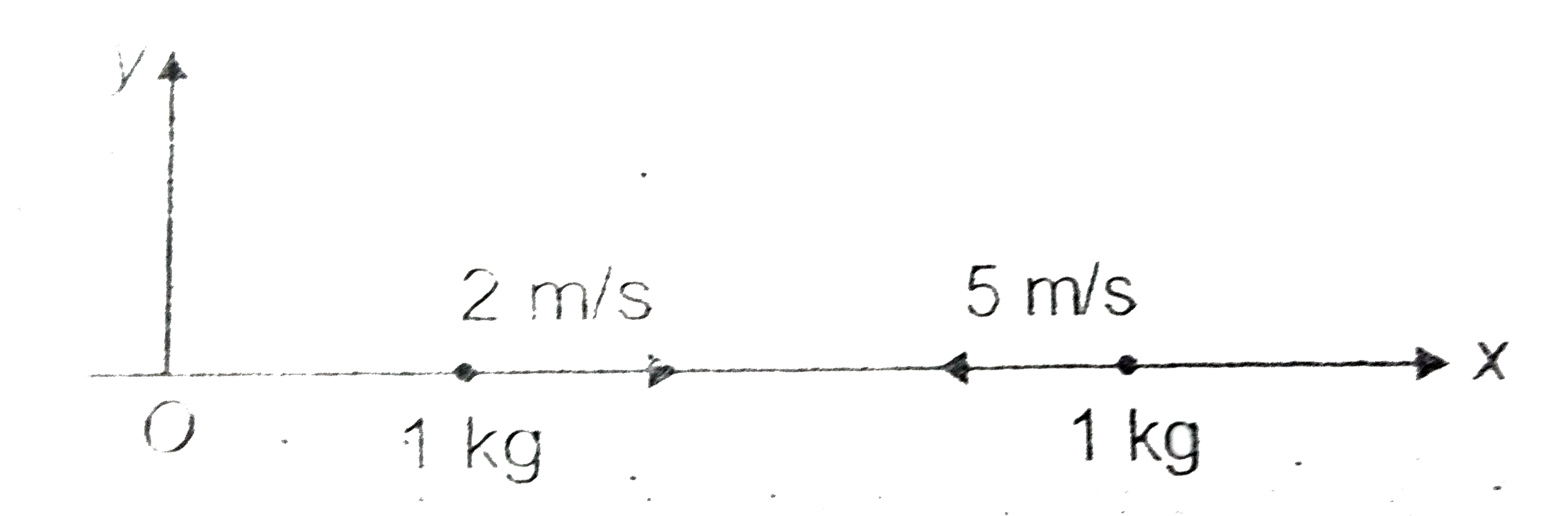 View Solution
View Solution

