Find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
The correct Answer is:A, B
To find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals, we can follow these steps:
Step 1: Understand the Geometry
We have a square plate with mass M and side length a. We want to find the moment of inertia about a diagonal of the square.
Step 2: Moment of Inertia About an Axis Through the Center
First, we need to find the moment of inertia of the square plate about an axis that is perpendicular to the plane of the square and passes through its center. According to the formula for a square plate, the moment of inertia IO about this axis is given by:
IO=16Ma2
Step 3: Moment of Inertia About the Axes Along the Sides
Next, we calculate the moment of inertia about an axis along one of the sides of the square. The moment of inertia IAB about this axis is:
IAB=13Ma2
Since the square is symmetric, the moment of inertia about the other side (let's call it IA′B′) is the same:
IA′B′=13Ma2
Step 4: Apply the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (in this case, the axis through the center O) is equal to the sum of the moments of inertia about two perpendicular axes in the plane (the axes along the sides of the square):
IO=IAB+IA′B′
Substituting the values we have:
IO=13Ma2+13Ma2=23Ma2
Step 5: Moment of Inertia About the Diagonal
Now, we need to find the moment of inertia about the diagonal. We will denote the moment of inertia about the diagonal as ID. By the perpendicular axis theorem, we can relate the moment of inertia about the diagonal to the moment of inertia about the axes along the sides:
IO=ID+ID
This simplifies to:
IO=2ID
Substituting our earlier result for IO:
23Ma2=2ID
Dividing both sides by 2 gives:
ID=13Ma2
Conclusion
Thus, the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals is:
ID=13Ma2
We have a square plate with mass M and side length a. We want to find the moment of inertia about a diagonal of the square.
First, we need to find the moment of inertia of the square plate about an axis that is perpendicular to the plane of the square and passes through its center. According to the formula for a square plate, the moment of inertia IO about this axis is given by:
IO=16Ma2
Next, we calculate the moment of inertia about an axis along one of the sides of the square. The moment of inertia IAB about this axis is:
IAB=13Ma2
IA′B′=13Ma2
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (in this case, the axis through the center O) is equal to the sum of the moments of inertia about two perpendicular axes in the plane (the axes along the sides of the square):
IO=IAB+IA′B′
Substituting the values we have:
IO=13Ma2+13Ma2=23Ma2
Now, we need to find the moment of inertia about the diagonal. We will denote the moment of inertia about the diagonal as ID. By the perpendicular axis theorem, we can relate the moment of inertia about the diagonal to the moment of inertia about the axes along the sides:
IO=ID+ID
This simplifies to:
IO=2ID
Substituting our earlier result for IO:
23Ma2=2ID
Dividing both sides by 2 gives:
ID=13Ma2
Thus, the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals is:
ID=13Ma2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
Knowledge Check
Find the momentof inertia of a uniform square plate of mass m and edge a about one of its diagonals.
AMl26BMl212CMl23DMl24
Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
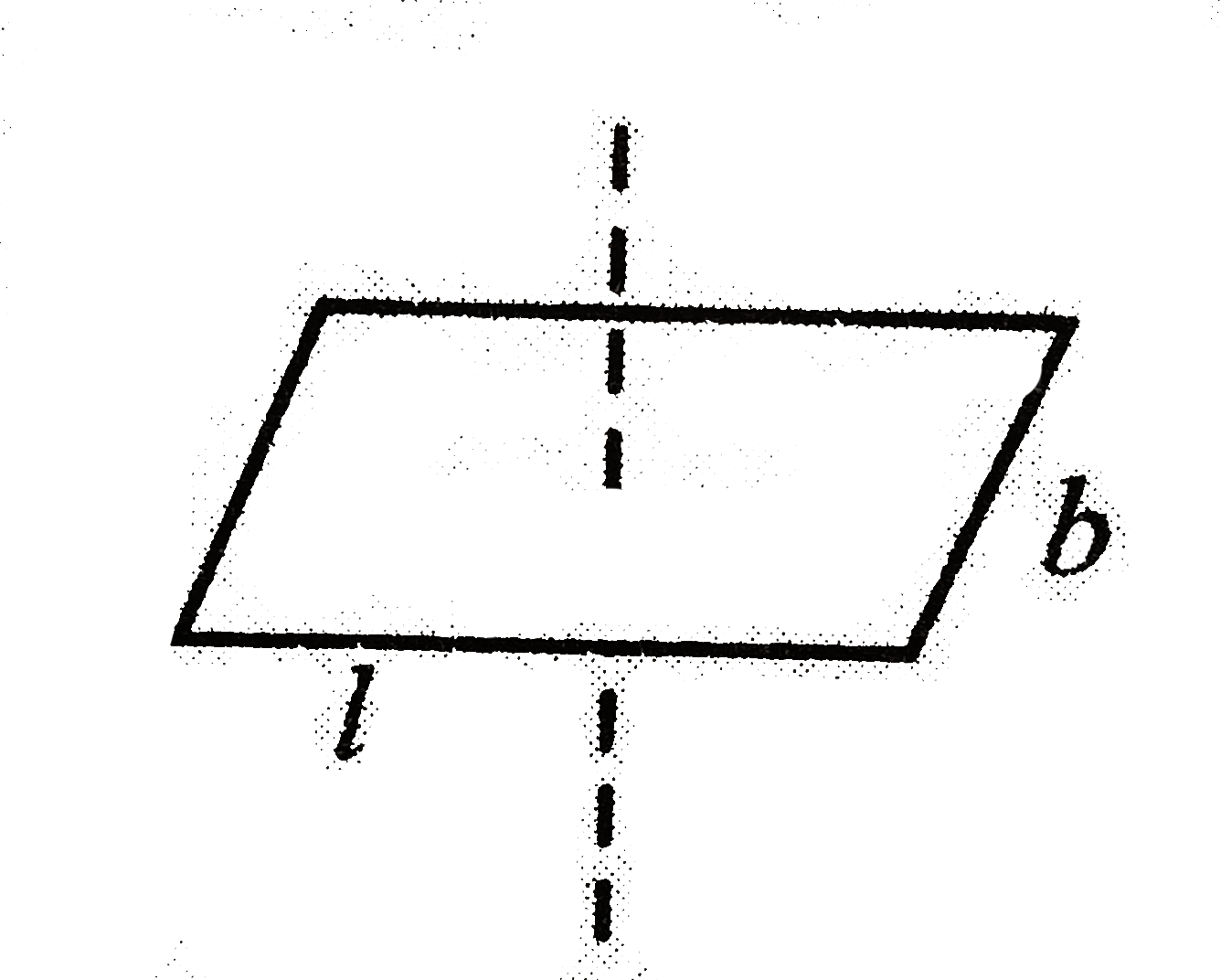
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View SolutionThe moment of inertia of a uniform solid regular tetrahedron of mass m and edge a, about its symmetry axis (i.e and axis passing through on evertex and the centre of the opposite face) is:
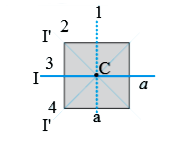
View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?
View SolutionMoment of inertia of a circular wire of mass M and radius R about its diameter is
View Solution
