Moment of inertia of a circular wire of mass M and radius R about its diameter is
MR2/2
MR2
2MR2
MR2/4
The correct Answer is:A
To find the moment of inertia of a circular wire of mass M and radius R about its diameter, we can follow these steps:
Step 1: Understand the Geometry
We have a circular wire that can be visualized as a thin ring. The wire has a mass M and a radius R. We need to calculate the moment of inertia about an axis that passes through the diameter of the ring.
Step 2: Use the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (let's call it the z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (the x-axis and y-axis) lying in the plane of the body. Mathematically, this can be expressed as:
Iz=Ix+Iy
Step 3: Moment of Inertia About the Center Axis
For a thin ring, the moment of inertia about an axis perpendicular to the plane of the ring (the z-axis) and passing through its center is given by:
Iz=MR2
Step 4: Symmetry of the Ring
Due to the symmetry of the ring, the moments of inertia about the two axes in the plane (the x-axis and y-axis) are equal:
Ix=Iy
Let’s denote the moment of inertia about the x-axis (or y-axis) as I. Therefore, we can rewrite the equation from the perpendicular axis theorem as:
Iz=I+I
or
Iz=2I
Step 5: Substitute and Solve
Now, substituting Iz into the equation:
MR2=2I
To find I, we rearrange the equation:
I=MR22
Conclusion
Thus, the moment of inertia of a circular wire of mass M and radius R about its diameter is:
I=MR22
We have a circular wire that can be visualized as a thin ring. The wire has a mass M and a radius R. We need to calculate the moment of inertia about an axis that passes through the diameter of the ring.
The perpendicular axis theorem states that for a planar body, the moment of inertia about an axis perpendicular to the plane (let's call it the z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (the x-axis and y-axis) lying in the plane of the body. Mathematically, this can be expressed as:
Iz=Ix+Iy
For a thin ring, the moment of inertia about an axis perpendicular to the plane of the ring (the z-axis) and passing through its center is given by:
Iz=MR2
Due to the symmetry of the ring, the moments of inertia about the two axes in the plane (the x-axis and y-axis) are equal:
Ix=Iy
Let’s denote the moment of inertia about the x-axis (or y-axis) as I. Therefore, we can rewrite the equation from the perpendicular axis theorem as:
Iz=I+I
or
Iz=2I
Now, substituting Iz into the equation:
MR2=2I
To find I, we rearrange the equation:
I=MR22
Thus, the moment of inertia of a circular wire of mass M and radius R about its diameter is:
I=MR22
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
Explore 26 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
Explore 17 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.
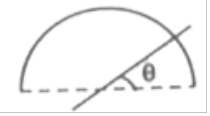
View SolutionThe moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle θ with the line joining its ends ( as shown ) is
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a uniform semicircular wire of mass 'M' and radius 'r' about a line perpendicular to the plane of the wire through the center is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View Solution