The surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
The correct Answer is:A, B, D
To find the moment of inertia I of a circular disc with a surface density that varies with the distance from the center, we can follow these steps:
Step 1: Define the surface density
The surface density ρ(r) is given by:
ρ(r)=A+Br
where A and B are constants, and r is the distance from the center of the disc.
Step 2: Consider an elemental ring
We consider a small elemental ring of radius r and thickness dr. The area of this ring is given by:
dA=2πrdr
Step 3: Find the mass of the elemental ring
The mass dm of the elemental ring can be expressed as:
dm=ρ(r)⋅dA=(A+Br)⋅(2πrdr)
Step 4: Express the moment of inertia of the ring
The moment of inertia dI of the elemental ring about the axis perpendicular to the plane of the disc through its center is:
dI=r2dm=r2⋅(A+Br)⋅(2πrdr)
This simplifies to:
dI=2πr2(A+Br)rdr=2π(Ar3+Br4)dr
Step 5: Integrate to find the total moment of inertia
To find the total moment of inertia I, we integrate dI from r=0 to r=a:
I=∫a0dI=∫a02π(Ar3+Br4)dr
Step 6: Calculate the integrals
We can separate the integral:
I=2π(∫a0Ar3dr+∫a0Br4dr)
Calculating each integral:
1. For ∫a0r3dr:
∫a0r3dr=(r44)a0=a44
2. For ∫a0r4dr:
∫a0r4dr=(r55)a0=a55
Step 7: Substitute back into the equation for I
Substituting the results of the integrals back into the equation for I:
I=2π(A⋅a44+B⋅a55)
Step 8: Final expression for the moment of inertia
Thus, the moment of inertia I of the circular disc about the axis perpendicular to the plane through its center is:
I=2πa4A4+2πa5B5
This can be simplified to:
I=πa4A2+2πa5B5
The surface density ρ(r) is given by:
ρ(r)=A+Br
where A and B are constants, and r is the distance from the center of the disc.
We consider a small elemental ring of radius r and thickness dr. The area of this ring is given by:
dA=2πrdr
The mass dm of the elemental ring can be expressed as:
dm=ρ(r)⋅dA=(A+Br)⋅(2πrdr)
The moment of inertia dI of the elemental ring about the axis perpendicular to the plane of the disc through its center is:
dI=r2dm=r2⋅(A+Br)⋅(2πrdr)
This simplifies to:
dI=2πr2(A+Br)rdr=2π(Ar3+Br4)dr
To find the total moment of inertia I, we integrate dI from r=0 to r=a:
I=∫a0dI=∫a02π(Ar3+Br4)dr
We can separate the integral:
I=2π(∫a0Ar3dr+∫a0Br4dr)
Calculating each integral:
1. For ∫a0r3dr:
∫a0r3dr=(r44)a0=a44
2. For ∫a0r4dr:
∫a0r4dr=(r55)a0=a55
Substituting the results of the integrals back into the equation for I:
I=2π(A⋅a44+B⋅a55)
Thus, the moment of inertia I of the circular disc about the axis perpendicular to the plane through its center is:
I=2πa4A4+2πa5B5
This can be simplified to:
I=πa4A2+2πa5B5
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
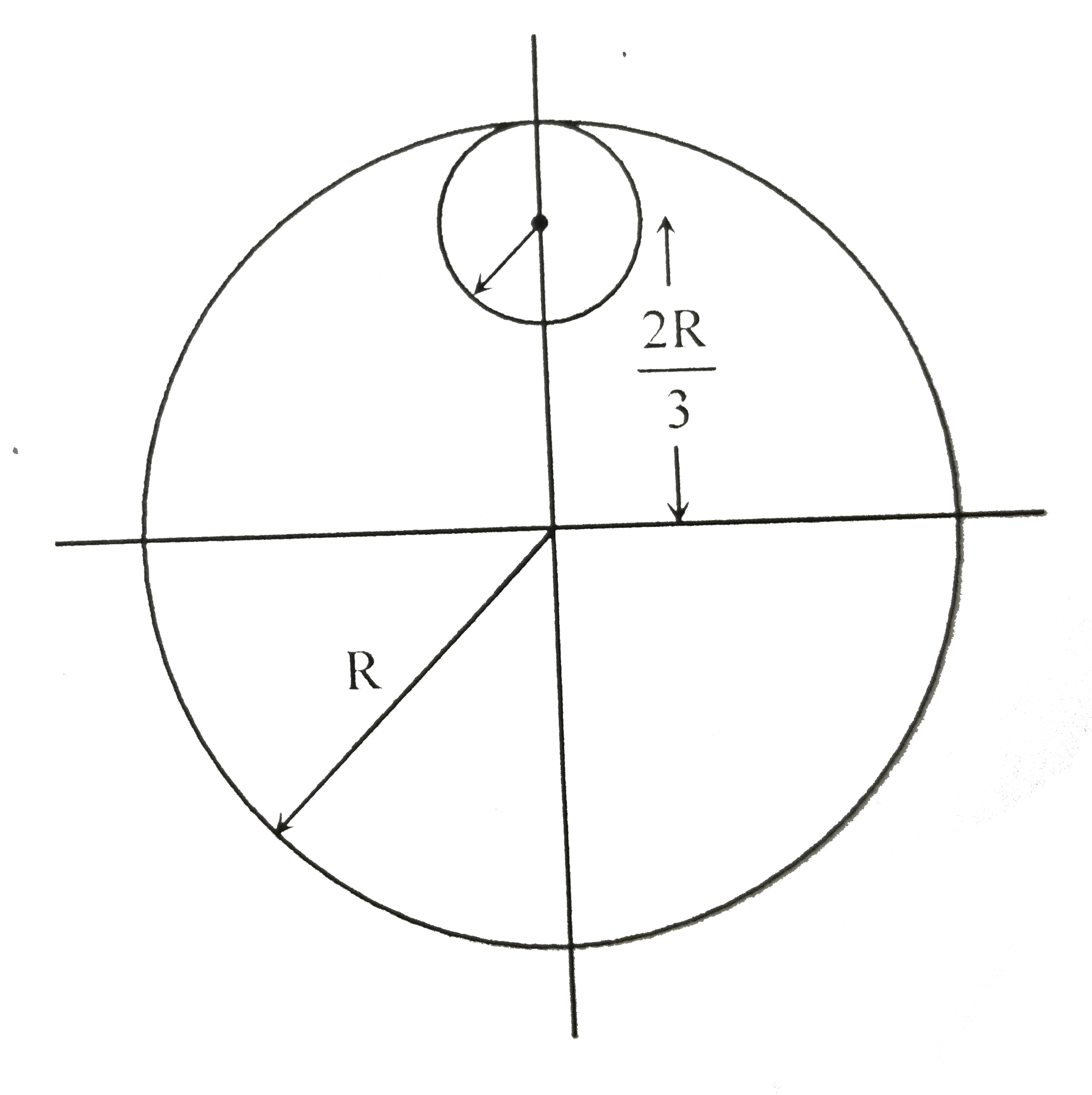 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
The moment of inertia of thin uniform circular disc about one of the diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its centre is
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA uniform disc of mass m and radius R has an additional rim of mass m as well as four symmetrically placed masses, each of mass m/4 tied at positions R/2 from the centre as shown in Fig. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
