Suppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
The correct Answer is:A, B, C
a. Angular momentum =mvr
conservation of linear momentum
μ=2mv−mv=mv
∴u=v=mvr
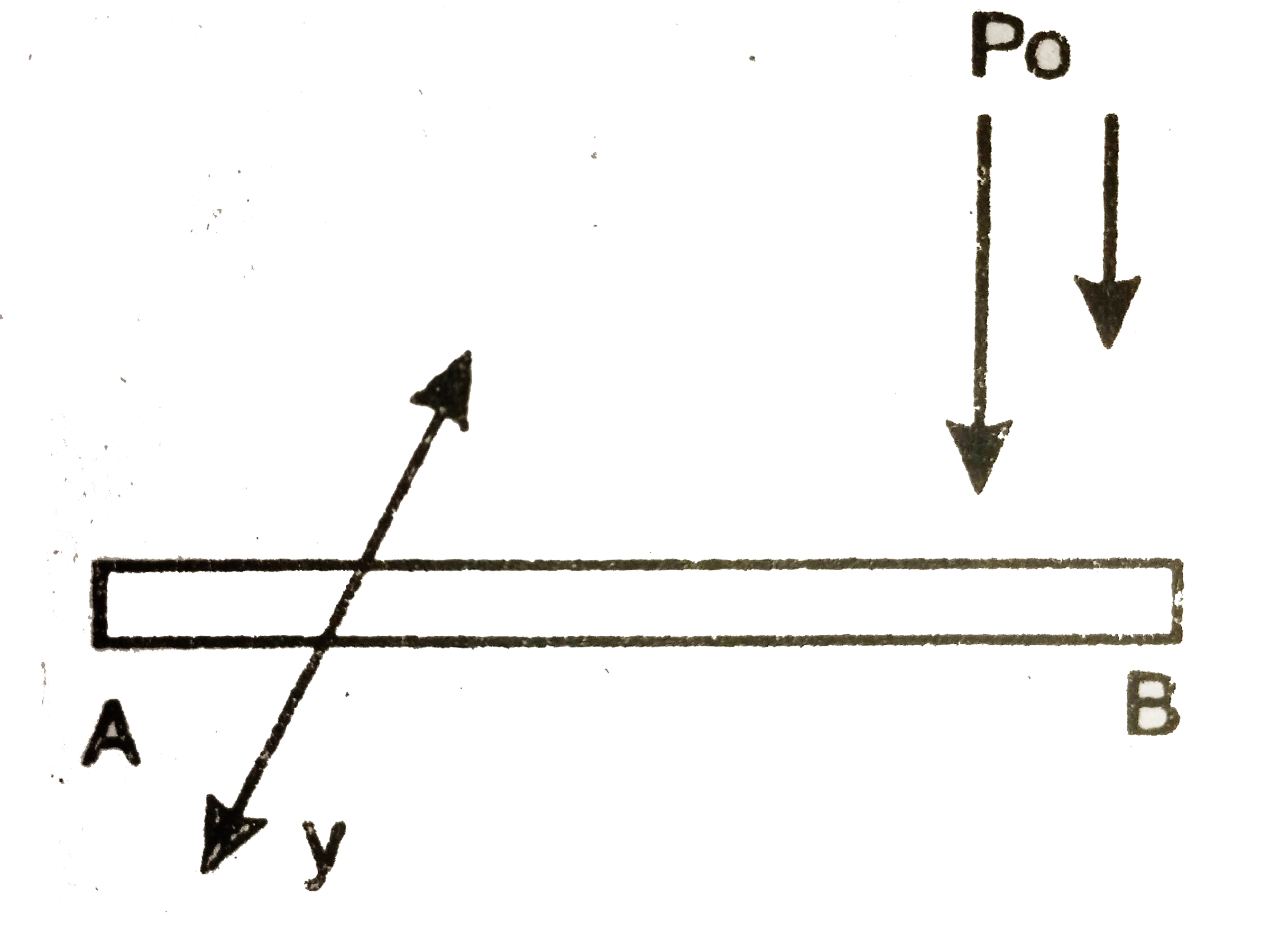
Velocity =sqrt(2gh)<br>andr=L/2<br>Angular momentum =m.sqrt(2gh.L/2<br>=(mLsqrt(gh))/sqrt2<br>Anga––rmomentum=lw<br>:.omega=angular velocity =L/I<br>or=I=(2mL^2)/4+(mL^2)/4=(3mL^2)/4<br>:. omega=(mLsqrtI(gh)/sqrt2)/(3mL^2/4)=sqrt(8gh)/(3L)<br>b.Whenthemass2mwilbeatthe⊤mostpositionandthemassmbetˆthelowestp∮.Theywillau→maticalyrotate.<br>∈thispositionthe→talgaion∈potentiale≠rgy<br>=2mgxx(L/2)-mg(L/2)<br>∴mgL/2=((1/2x2mL^2))/4xx((8gh)/(9gL^2))<br>rarr h=(3L)/2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
Two small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.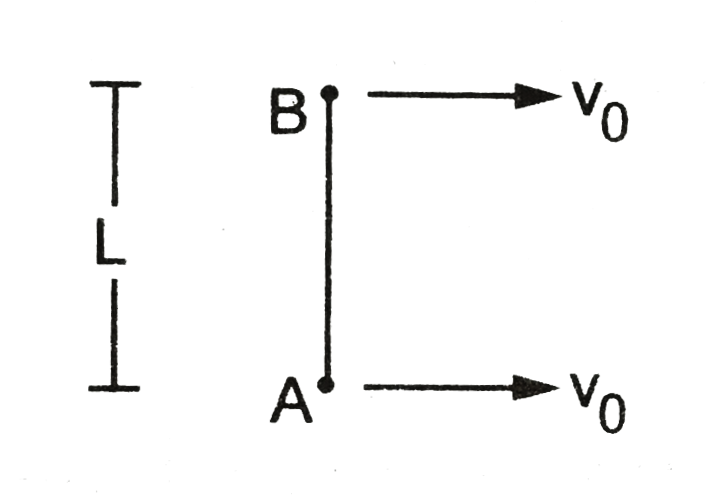
View Solution
Knowledge Check
Two balls of same mass are released simultaneously from heights h & 2h from the ground level. The balls collide with the floor & stick to it. Then the velocity-time graph of centre of mass of the two balls is best represented by :
A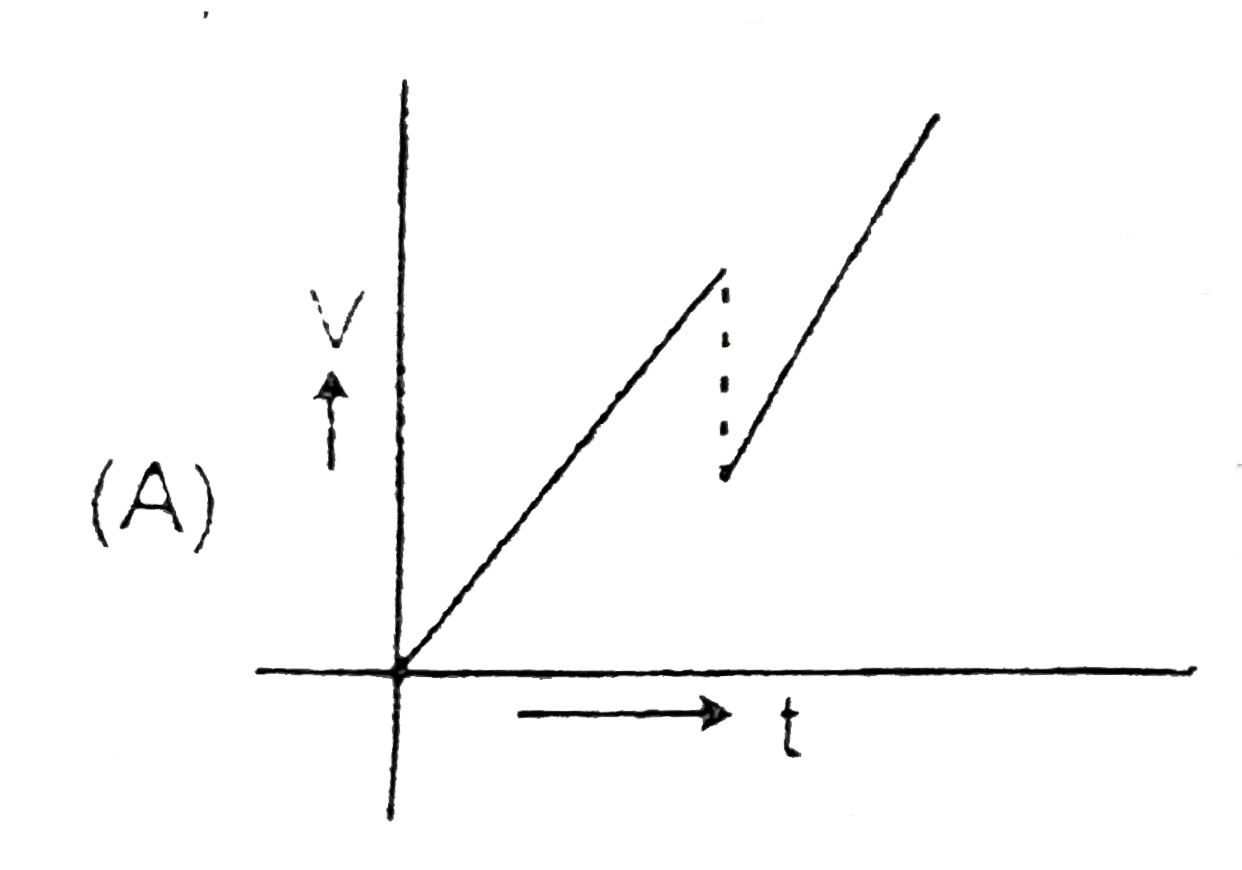 B
B C
C D
D

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθ
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionTwo balls of same mass are released simultaneously from heights h & 2h from the ground level. The balls collide with the floor & stick to it. Then the velocity-time graph of centre of mass of the two balls is best represented by :
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionTwo 2.00 kg balls are attached to the ends of a thin rod of length 50.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal (Fig. 10-87), a 50.0 g wad of wet putty drops onto one of the balls, hitting it with a speed of 3.00 m/s and then sticking to it. (a) What is the angular speed of the system just after the putty wad hits? (b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before? ( c) Through what angle will the system rotate before it momentarily stops?

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
