Two small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
The correct Answer is:A, B, C
Here Net torque =0 ltbrlt snce the angular momentum is conserved.
S, I1w1=I2w2

2mL^2.w=3mL^2w'<br>rarr w'=2/3w
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.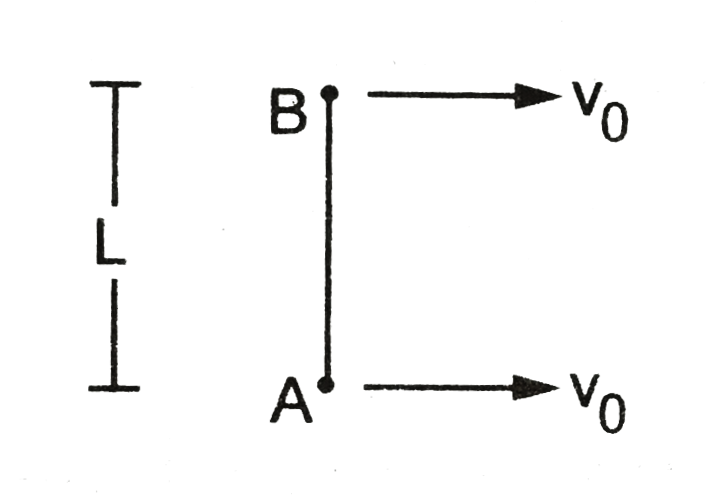
View SolutionSuppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
View Solution
Knowledge Check
Two particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
AqmB2qmCq2mDqπmA horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heatTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
Aq2mBqmC2qmDqπm
Two small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
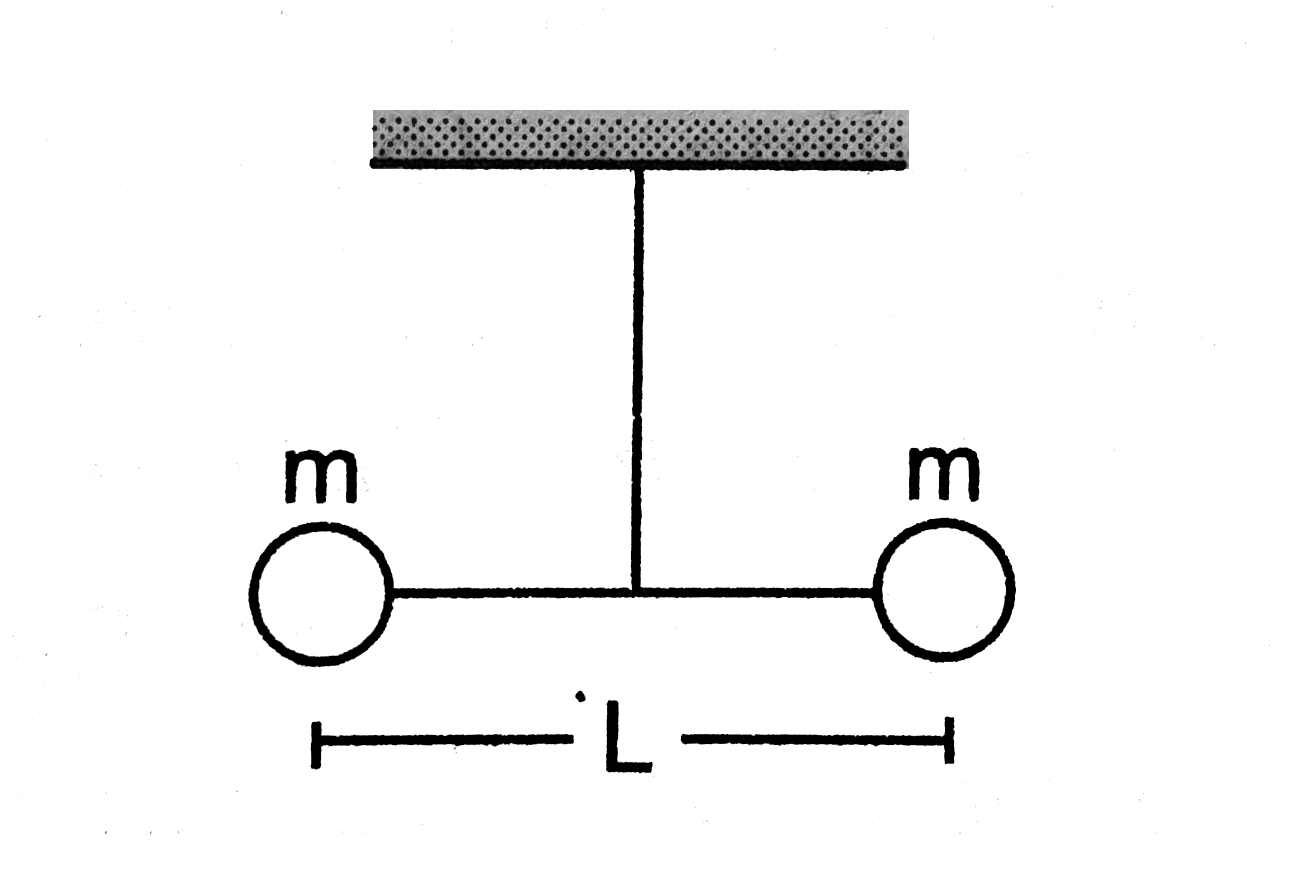
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
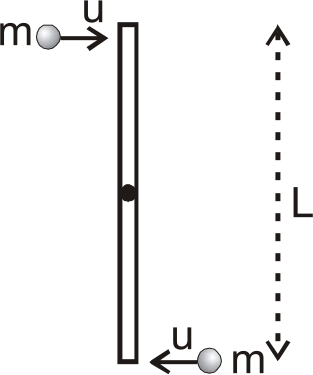
View SolutionA uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
