Is it necessary for the plane of the orbit of a satellite to pass through the Centre of the earth?
To determine whether it is necessary for the plane of the orbit of a satellite to pass through the center of the Earth, we can analyze the concept of gravitational forces and orbital mechanics.
1. Understanding Satellite Orbits:
A satellite orbits a planet due to the gravitational force acting between the satellite and the planet. This gravitational force provides the necessary centripetal force that keeps the satellite in orbit.
Hint: Remember that gravitational force is always directed towards the center of the planet.
2. Gravitational Force and Center of Mass:
The gravitational force acts as if all the mass of the Earth is concentrated at its center. Therefore, for a satellite, the center of the Earth is the point towards which the gravitational force is directed.
Hint: Consider how the gravitational force affects the motion of the satellite in different orbital planes.
3. Orbital Plane Orientation:
The plane of the orbit of a satellite can be inclined at various angles with respect to the equatorial plane of the Earth. However, for stable orbits, the gravitational force must act perpendicular to the velocity of the satellite at any point in its orbit.
Hint: Think about how changing the angle of the orbit might affect the gravitational force acting on the satellite.
4. Centripetal Force Requirement:
For a satellite to maintain a stable orbit, the net force acting on it (which is the gravitational force) must always point towards the center of the Earth. If the plane of the orbit does not intersect the center of the Earth, the gravitational force may not provide the necessary centripetal force for a stable orbit.
Hint: Visualize the satellite's path and how the gravitational pull influences its trajectory.
5. Potential for Capture by Other Bodies:
If the orbit does not pass through the center of the Earth, the satellite may not remain in a stable orbit and could potentially be captured by other celestial bodies or escape into space.
Hint: Consider the implications of gravitational interactions with other bodies in the solar system.
Conclusion:
Yes, it is necessary for the plane of the orbit of a satellite to pass through the center of the Earth to ensure that the gravitational force acts as the centripetal force required for a stable orbit. If the orbit does not pass through the center, the satellite may not maintain its orbit and could be influenced by other gravitational forces.
A satellite orbits a planet due to the gravitational force acting between the satellite and the planet. This gravitational force provides the necessary centripetal force that keeps the satellite in orbit.
The gravitational force acts as if all the mass of the Earth is concentrated at its center. Therefore, for a satellite, the center of the Earth is the point towards which the gravitational force is directed.
The plane of the orbit of a satellite can be inclined at various angles with respect to the equatorial plane of the Earth. However, for stable orbits, the gravitational force must act perpendicular to the velocity of the satellite at any point in its orbit.
For a satellite to maintain a stable orbit, the net force acting on it (which is the gravitational force) must always point towards the center of the Earth. If the plane of the orbit does not intersect the center of the Earth, the gravitational force may not provide the necessary centripetal force for a stable orbit.
If the orbit does not pass through the center of the Earth, the satellite may not remain in a stable orbit and could potentially be captured by other celestial bodies or escape into space.
Yes, it is necessary for the plane of the orbit of a satellite to pass through the center of the Earth to ensure that the gravitational force acts as the centripetal force required for a stable orbit. If the orbit does not pass through the center, the satellite may not maintain its orbit and could be influenced by other gravitational forces.
Topper's Solved these Questions
Similar Questions
Statement-1: The plane of the orbit of an artificial satellite must contain the centre of the Earth.
Statement-2: For an artificial satellite, the necessary centripetal force is provided by gravity.
View SolutionTwo satellites A and B of the same mass are revolving around the earth in the concentric circular orbits such that the distance of satellite B from the centre of the earth is thrice as compared to the distance of the satellite A from the centre of the earth. The ratio of the centripetal force acting on B as compared to that on A is
View Solution
Knowledge Check
The orbit of geostationary satellite is circular, the time period of satellite depeds on (i) mass of the satellite, (ii) mass of earth, (iii) radius of the orbit and (iv) height of the satellite from the surface of the earth
A(i) onlyB(i) and (ii)C(i),(ii) and (iii)D(ii),(iii) and (iv)A geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
A3√2hB1.5√2hC6√2hD12√2h
A geostationary satellite is orbiting the earth at a height of 6R above the surface of earth where R is the radius of the earth .The time period of another satellite at a distance of 3.5R from the Centre of the earth is ….. hours.
View SolutionWhat impulse need to be given to a body of mass m, released from the surface of earth along a straight tunnel passing through centre of earth, at the centre of earth, to bring it to rest. (Mass of earth M, radius of earth R)

View SolutionAssertion : Plane of a satellite always passes through the centre of earth
Reason : Gravitational force on satellite is always towards centre of earth.
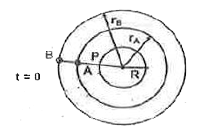
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
View SolutionIf an artificial satellite is moving in a circular orbit around earth with speed equal to one fourth of Ve from earth, then height of the satellite above the surface of the earth is
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View Solution
