Figure shows the elipticla path of a planet about the sun. The two shaded parts have equal area. If t1andt2 be the tim taken by the planet to go from a to b and from c to d respectively
t1<t2
t1=t2
t1>t2
insufficient information to deduce the relation between t1andt2 
The correct Answer is:B
To solve the problem, we need to apply Kepler's Second Law of Planetary Motion, which states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
1. Identify the Areas:
- We have two shaded areas in the elliptical path of the planet: Area A1 (from point A to point B) and Area A2 (from point C to point D). According to the problem, these two areas are equal: A1 = A2.
2. Apply Kepler's Second Law:
- According to Kepler's Second Law, the area swept out by the planet in a given time interval is constant. This can be mathematically expressed as:
dA1dt1=dA2dt2
- Here, dA1 is the area swept out from A to B in time t1, and dA2 is the area swept out from C to D in time t2.
3. Set Up the Equation:
- Since A1 = A2, we can substitute this into our equation:
A1t1=A2t2
- This simplifies to:
A1t1=A1t2
4. Cancel the Areas:
- Since A1 is equal to A2, we can cancel them out from both sides of the equation:
1t1=1t2
5. Conclude the Relationship:
- From the equation above, we can conclude that:
t1=t2
- This indicates that the time taken by the planet to travel from A to B (t1) is equal to the time taken to travel from C to D (t2).
Final Answer:
Thus, the correct conclusion is that t1=t2.
---
- We have two shaded areas in the elliptical path of the planet: Area A1 (from point A to point B) and Area A2 (from point C to point D). According to the problem, these two areas are equal: A1 = A2.
- According to Kepler's Second Law, the area swept out by the planet in a given time interval is constant. This can be mathematically expressed as:
dA1dt1=dA2dt2
- Here, dA1 is the area swept out from A to B in time t1, and dA2 is the area swept out from C to D in time t2.
- Since A1 = A2, we can substitute this into our equation:
A1t1=A2t2
- This simplifies to:
A1t1=A1t2
- Since A1 is equal to A2, we can cancel them out from both sides of the equation:
1t1=1t2
- From the equation above, we can conclude that:
t1=t2
- This indicates that the time taken by the planet to travel from A to B (t1) is equal to the time taken to travel from C to D (t2).
Thus, the correct conclusion is that t1=t2.
Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -2
6 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - worked out Examples
13 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
Similar Questions
The figure shows elliptical orbit of a plant P about the sun S. The shaded area CSD is twice tha shaded area ASB. If t1 is the time taken by the planet to move from C to D and t2 is the time to move from A to B, determine the ratio t1/t2
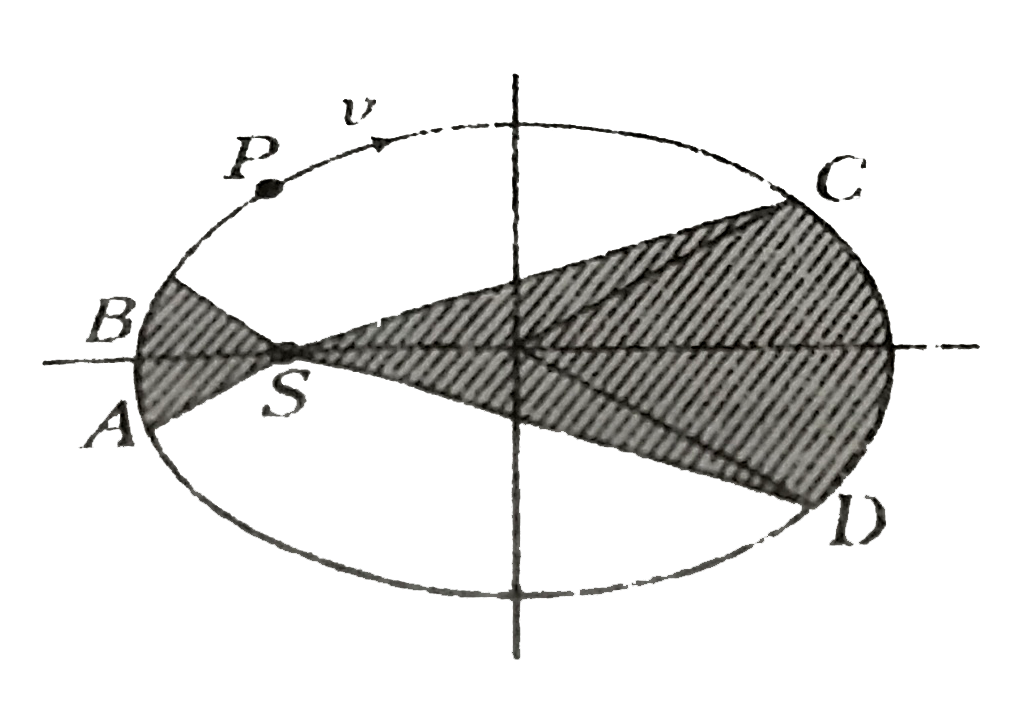
View Solution_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:
View Solution
Knowledge Check
_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:At1=t2Bt1=2t2Ct1=4t2Dt1>t2
Figure shows the motion of a planet around the Sun S in an elliptical orbit with the Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d, respectively then

View SolutionFigure shows the motion of a planet around the Sun S in an elliptical orbit with the Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d, respectively then

View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and t2 in moving from A to B and from C to D respectively, then
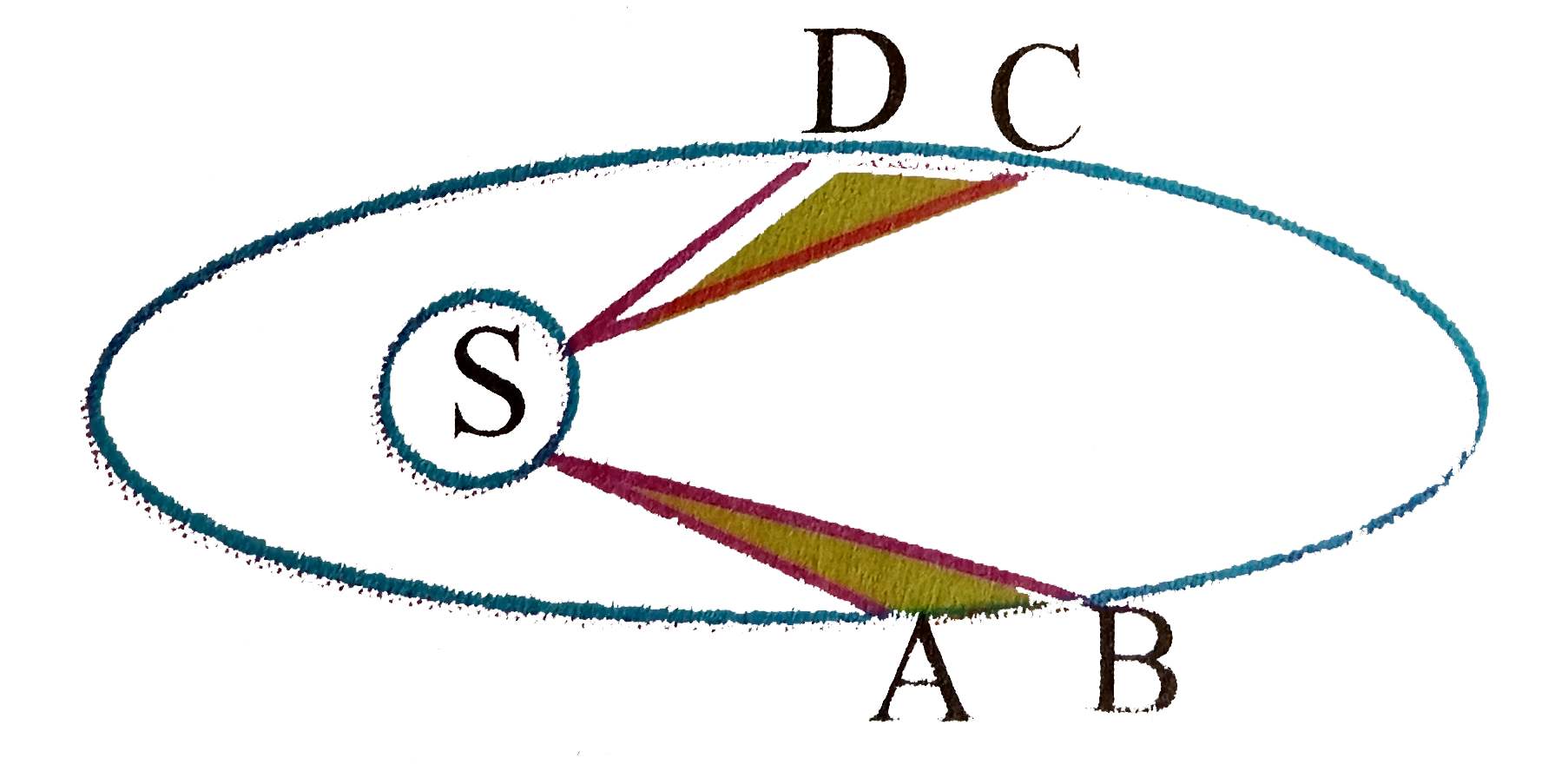
View Solution_E01_134_Q01.png)
Figure elliptical path abcd of a planet around the sun S such that the area of Delta csa is 14 the area of the ellipse, (see figure) with db as the semimajor axis, and ca as the semiminor axis if t1 is the time taken for planet to go over path abc and t2 for path taken over cda then:
View SolutionThe figure represents an elliptical orbit a planet around sun. The planet takes time T1 to travel from A to B and it takes time T2 to travel from C to D. If the area CSD is double that of area ASB, them

View SolutionAstronomers observe two separate solar systems each consisting of a planet orbiting a sun. The two orbits are circular and have the same radius R. It is determined that the planets have angular momenta of the same magnitude L about their suns, and that the orbital periods are in the ratio of three to one, i.e. T1=3T2. The ratio m1/m2 of the masses of the two planets is
View SolutionIn figure shown below, the time taken by the projectile to reach from A to B is t then, the distance AB is equal to
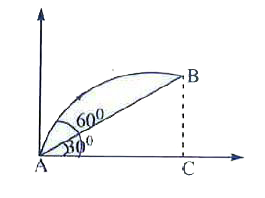
View Solution
