Let V and E denote the gravitational potential and gravitational field at a point. It is possile to have
The correct Answer is:A, C, D
To solve the problem, we need to analyze the possible scenarios for gravitational potential (V) and gravitational field (E) at a point in relation to a spherical shell.
1. Understanding Gravitational Potential (V) and Gravitational Field (E):
- Gravitational potential (V) at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
- Gravitational field (E) at a point is defined as the force experienced by a unit mass placed at that point.
2. Case A: V = 0 and E = 0:
- At infinity, the gravitational potential (V) is defined to be zero. Since the gravitational field (E) is derived from the potential, it is also zero at infinity.
- Therefore, it is possible to have both V = 0 and E = 0 at a point at infinity.
- Conclusion: This case is possible.
3. Case B: V = 0 and E ≠ 0:
- If we consider a point just outside a spherical shell, the potential (V) is not zero, but the gravitational field (E) is not zero either.
- Hence, it is not possible to have V = 0 while E is not zero.
- Conclusion: This case is not possible.
4. Case C: V ≠ 0 and E = 0:
- Inside a spherical shell, the gravitational field (E) is zero, but the potential (V) is constant and does not equal zero.
- Thus, it is possible to have V ≠ 0 while E = 0.
- Conclusion: This case is possible.
5. Case D: V ≠ 0 and E ≠ 0:
- Outside the spherical shell, both the gravitational potential (V) and gravitational field (E) are non-zero.
- Therefore, it is possible to have both V ≠ 0 and E ≠ 0.
- Conclusion: This case is possible.
Final Summary of Cases:
- Case A: Possible (V = 0, E = 0)
- Case B: Not possible (V = 0, E ≠ 0)
- Case C: Possible (V ≠ 0, E = 0)
- Case D: Possible (V ≠ 0, E ≠ 0)
- Gravitational potential (V) at a point is defined as the work done in bringing a unit mass from infinity to that point without any acceleration.
- Gravitational field (E) at a point is defined as the force experienced by a unit mass placed at that point.
- At infinity, the gravitational potential (V) is defined to be zero. Since the gravitational field (E) is derived from the potential, it is also zero at infinity.
- Therefore, it is possible to have both V = 0 and E = 0 at a point at infinity.
- Conclusion: This case is possible.
- If we consider a point just outside a spherical shell, the potential (V) is not zero, but the gravitational field (E) is not zero either.
- Hence, it is not possible to have V = 0 while E is not zero.
- Conclusion: This case is not possible.
- Inside a spherical shell, the gravitational field (E) is zero, but the potential (V) is constant and does not equal zero.
- Thus, it is possible to have V ≠ 0 while E = 0.
- Conclusion: This case is possible.
- Outside the spherical shell, both the gravitational potential (V) and gravitational field (E) are non-zero.
- Therefore, it is possible to have both V ≠ 0 and E ≠ 0.
- Conclusion: This case is possible.
- Case A: Possible (V = 0, E = 0)
- Case B: Not possible (V = 0, E ≠ 0)
- Case C: Possible (V ≠ 0, E = 0)
- Case D: Possible (V ≠ 0, E ≠ 0)
Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Objective -1
16 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
Similar Questions
Let V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
View SolutionDefine gravitational potential and gravitational potential energy.
View Solution
Knowledge Check
Gravitational potential energy = ....
AmghB12mv2C2mghDnone of these
Define gravitational potential and its unit.
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionObtain an expression for the gravitational potential.
View SolutionThe gravitational potential energy is maximum at :
View SolutionGravitational field due to a solid sphere
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
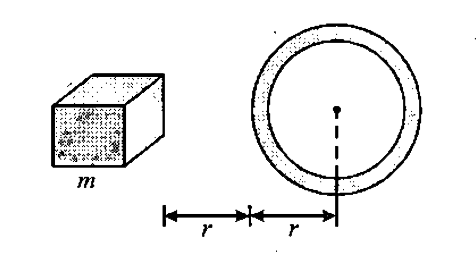
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View SolutionFind the gravitational potential at a point where the gravitational field intensity is zero due to two particles of masses m1=1kg and m2=4kg separated through a distance l=3m ?
View Solution
