The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
The correct Answer is:A, B
To find the tension in the string of a simple pendulum at the lowest point in its path, we can follow these steps:
Step 1: Identify the forces acting on the bob
At the lowest point of the pendulum's swing, two forces act on the bob:
- The gravitational force (weight) acting downward, Fg=mg
- The tension in the string acting upward, T
Step 2: Calculate the weight of the bob
The mass of the bob is given as 100 g, which we need to convert to kilograms:
m=100g=0.1kg
Now, we can calculate the weight:
Fg=mg=0.1kg×9.8m/s2=0.98N
Step 3: Use centripetal force equation
At the lowest point, the net force acting on the bob is the centripetal force required to keep it moving in a circular path. The centripetal force is given by:
Fc=mv2r
where:
- v=1.4m/s (speed at the lowest point)
- r=1m (length of the pendulum)
Substituting the values:
Fc=0.1kg×(1.4m/s)21m=0.1×1.961=0.196N
Step 4: Write the equation for tension
At the lowest point, the tension in the string must support both the weight of the bob and provide the necessary centripetal force. Therefore, we can express the tension as:
T=Fg+Fc
Substituting the values we calculated:
T=0.98N+0.196N=1.176N
Final Answer
The tension in the string at the lowest point is:
T=1.176N
---
At the lowest point of the pendulum's swing, two forces act on the bob:
- The gravitational force (weight) acting downward, Fg=mg
- The tension in the string acting upward, T
The mass of the bob is given as 100 g, which we need to convert to kilograms:
m=100g=0.1kg
Now, we can calculate the weight:
Fg=mg=0.1kg×9.8m/s2=0.98N
At the lowest point, the net force acting on the bob is the centripetal force required to keep it moving in a circular path. The centripetal force is given by:
Fc=mv2r
where:
- v=1.4m/s (speed at the lowest point)
- r=1m (length of the pendulum)
Fc=0.1kg×(1.4m/s)21m=0.1×1.961=0.196N
At the lowest point, the tension in the string must support both the weight of the bob and provide the necessary centripetal force. Therefore, we can express the tension as:
T=Fg+Fc
Substituting the values we calculated:
T=0.98N+0.196N=1.176N
The tension in the string at the lowest point is:
T=1.176N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -26videos
CIRCULAR MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions90videos
FLUID MECHANICS
Similar Questions
A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionSuppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cosθ=1−θ22andsinθ=θ for small theta.
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum having a bob of mass m under goes small oscillations with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionA simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.
 View Solution
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘ true
falseView SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
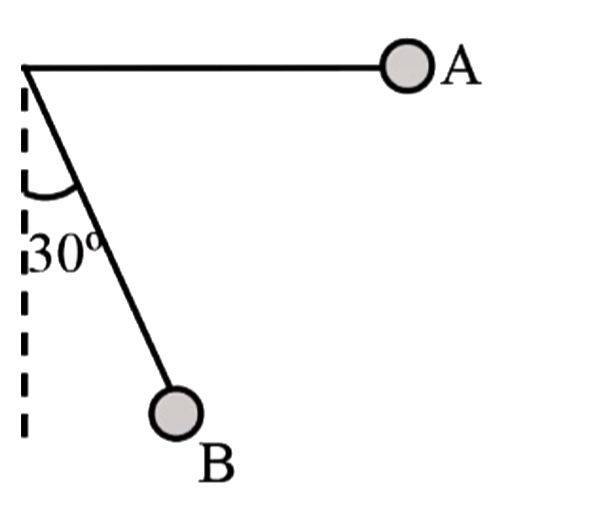 View Solution
View Solution

