Consider the equations
P=Lim△s→0F△SandP1−P2=ρgz
In an elevator acceleratin upward
both the equations are valid
the first is valid but not the second
the second is valid but not the first
both are invalid
The correct Answer is:B
To solve the problem, we need to analyze the two equations given in the context of an elevator that is accelerating upward.
Step 1: Understand the first equation
The first equation is given as:
P=limΔS→0FΔS
This equation represents the definition of pressure P as the limit of force F applied over an area ΔS as the area approaches zero. This definition is universally valid for pressure in any fluid, regardless of the conditions.
Step 2: Analyze the second equation
The second equation is:
P1−P2=ρgz
This equation relates the pressure difference P1−P2 between two points in a fluid to the density ρ, gravitational acceleration g, and the height difference z between those two points.
Step 3: Consider the effect of upward acceleration
When the elevator is accelerating upward, the effective gravitational acceleration changes. The effective gravitational acceleration g′ becomes:
g′=g+a
where a is the upward acceleration of the elevator.
Step 4: Modify the second equation for upward acceleration
Given that the effective gravitational acceleration is now g+a, we can modify the second equation:
P1−P2=ρ(g+a)z
This means that the pressure difference in the fluid must account for the additional acceleration due to the upward movement of the elevator.
Step 5: Conclusion about the validity of the equations
1. The first equation P=limΔS→0FΔS is always valid.
2. The second equation P1−P2=ρgz is not valid in the case of an upward accelerating elevator, as it does not account for the additional acceleration a.
Final Answer
Thus, the first equation is valid, while the second equation is not valid when the elevator is accelerating upward.
---
The first equation is given as:
P=limΔS→0FΔS
This equation represents the definition of pressure P as the limit of force F applied over an area ΔS as the area approaches zero. This definition is universally valid for pressure in any fluid, regardless of the conditions.
The second equation is:
P1−P2=ρgz
This equation relates the pressure difference P1−P2 between two points in a fluid to the density ρ, gravitational acceleration g, and the height difference z between those two points.
When the elevator is accelerating upward, the effective gravitational acceleration changes. The effective gravitational acceleration g′ becomes:
g′=g+a
where a is the upward acceleration of the elevator.
Given that the effective gravitational acceleration is now g+a, we can modify the second equation:
P1−P2=ρ(g+a)z
This means that the pressure difference in the fluid must account for the additional acceleration due to the upward movement of the elevator.
1. The first equation P=limΔS→0FΔS is always valid.
2. The second equation P1−P2=ρgz is not valid in the case of an upward accelerating elevator, as it does not account for the additional acceleration a.
Thus, the first equation is valid, while the second equation is not valid when the elevator is accelerating upward.
Topper's Solved these Questions
Similar Questions
Consider the equation p=5−2q−3
Greatest sat of all possible values of p for q∈R is
View SolutionConsider two points P1(2,7) and P2(6,15). Write the equation and draw a straight line through these points.
View SolutionConsider the equation p=5−2q−3
If p=|r|+5, then number of possible ordered pair (r,q) is, are
View SolutionConsider the equation p=5−2q−3
Ifp=4 then possible values of q are
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
View SolutionA container having two immiscible liquids of densities 'p' and '2p' moves with an upward acceleration a=g The values of PQ−P0 is (where P0 = atmospheric pressure)
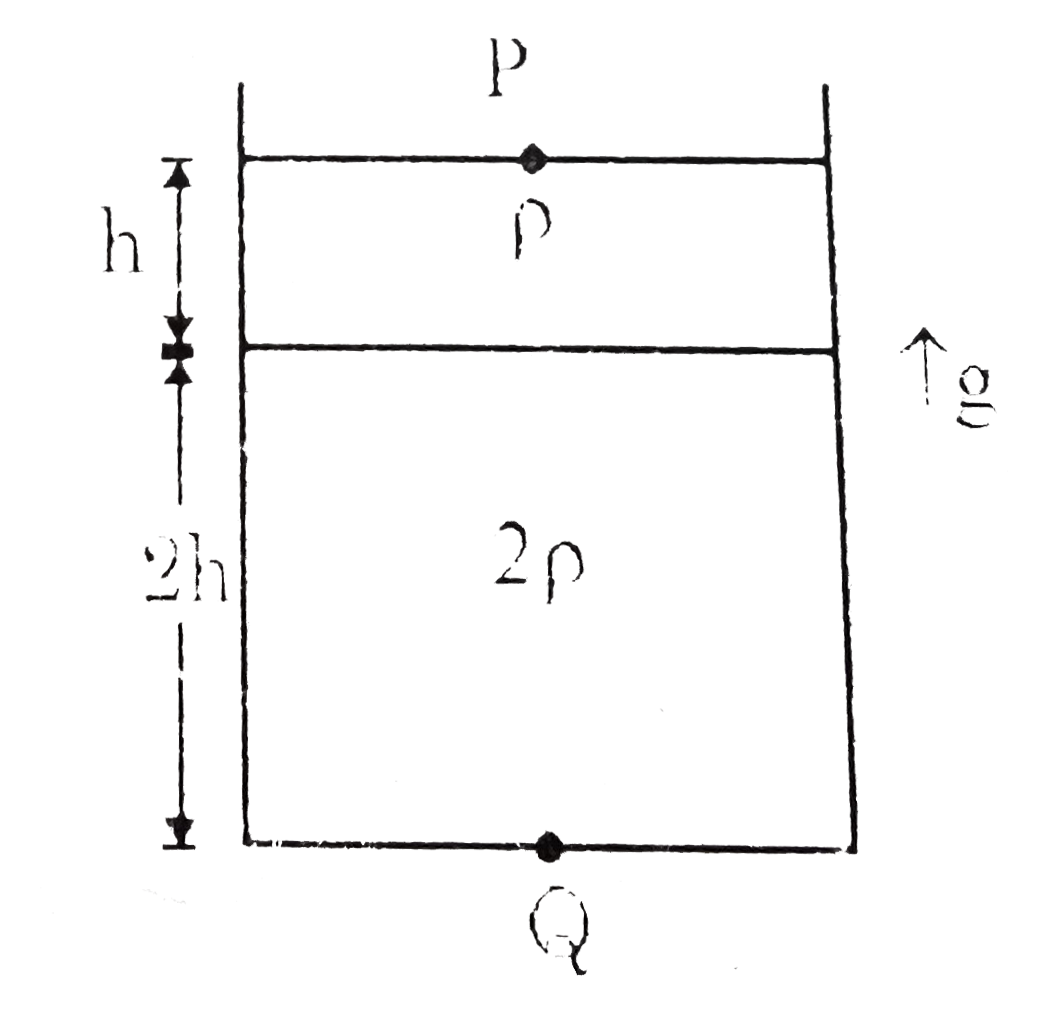
View SolutionIn the derivation of P1−P2=ρgz it was asumed that the liquid is incompressible. Why will this equation not be stictly valid for a compressible liquid?
View SolutionIf p1=0andp2=0 be two non-parallel planes, then the equation p1+λp2=0,λ∈R represents the family of all planes through the line of intersection of the planes p1=0andp2=0 except the plane :
View SolutionIf p, q, r are in G.P. and the equations, px2+2qx+r=0and dx2+2ex+f=0have a common root, then show that dp,eq,frare in A.P.
View SolutionConsider two intersecting (non-perpendicular lines L1=0andL2=0 and a point P1. Image of P1 and L1=0 is P2, image of P2 in L2=0 is P3 , image of P3 in L1 =0 is P4 and so on. Which of the following statements are incorrect ?
View Solution
