In the derivation of P1−P2=ρgz it was asumed that the liquid is incompressible. Why will this equation not be stictly valid for a compressible liquid?
To understand why the equation P1−P2=ρgh is not strictly valid for compressible liquids, we can break down the reasoning step by step.
1. Understanding the Equation:
The equation P1−P2=ρgh is derived under the assumption that the liquid is incompressible. Here, P1 and P2 are the pressures at two different points in a fluid column, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height difference between the two points.
2. Assumption of Incompressibility:
In the derivation of this equation, it is assumed that the density ρ of the fluid remains constant throughout the fluid column. This is a valid assumption for incompressible fluids, where the density does not change with pressure or height.
3. Behavior of Compressible Liquids:
For compressible liquids (like gases), the density is not constant. It varies with pressure and temperature. As the fluid moves through different heights or pressure conditions, its density can change significantly.
4. Impact of Density Variation:
Because the density ρ is variable in compressible fluids, the value of P1−P2 cannot be simplified to ρgh as it would be for incompressible fluids. At different heights in a compressible fluid, the density at point 1 (ρ1) may differ from the density at point 2 (ρ2), which means the pressure difference cannot be expressed with a single constant density.
5. Conclusion:
Therefore, the equation P1−P2=ρgh is not strictly valid for compressible liquids because the density varies with height and pressure, leading to different values of pressure at the same height in a compressible fluid.
Summary:
The equation P1−P2=ρgh assumes constant density, which is not the case for compressible liquids where density varies with pressure and height.
The equation P1−P2=ρgh is derived under the assumption that the liquid is incompressible. Here, P1 and P2 are the pressures at two different points in a fluid column, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height difference between the two points.
In the derivation of this equation, it is assumed that the density ρ of the fluid remains constant throughout the fluid column. This is a valid assumption for incompressible fluids, where the density does not change with pressure or height.
For compressible liquids (like gases), the density is not constant. It varies with pressure and temperature. As the fluid moves through different heights or pressure conditions, its density can change significantly.
Because the density ρ is variable in compressible fluids, the value of P1−P2 cannot be simplified to ρgh as it would be for incompressible fluids. At different heights in a compressible fluid, the density at point 1 (ρ1) may differ from the density at point 2 (ρ2), which means the pressure difference cannot be expressed with a single constant density.
Therefore, the equation P1−P2=ρgh is not strictly valid for compressible liquids because the density varies with height and pressure, leading to different values of pressure at the same height in a compressible fluid.
The equation P1−P2=ρgh assumes constant density, which is not the case for compressible liquids where density varies with pressure and height.
Topper's Solved these Questions
Similar Questions
A : Equation ofcontinuity is A1v1ρ1=A2v2ρ2 (symbols have their usual meanings).
R : Equation of continuity is valid only for incompressible liquids.
View SolutionGive reason to explain why:
Gases are so easily compressible whereas it is impossible to compress a solid or a liquid.
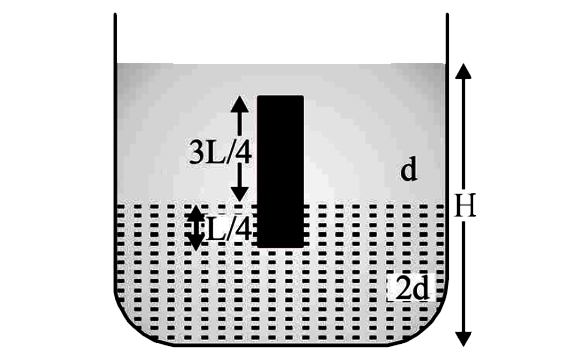
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
View SolutionIn the reaction of p-chlorotoluene with KNH2 is liquid NH3 the major product is .
View SolutionA liquid of volume of 100L and at the external pressure of 10atm−Lt the liquid is confined inside an adiabatic bath. External pressure of the liquid is suddenly increased to 100atm and the liquid gets compressed by 1L against this pressure then find,
(i) Work (ii) ΔU (iii) ΔH
View SolutionSTATEMENT - 1 Bernoulli's theorem is conversation of energy
because
STATEMENT - 2 Mass flowing per second at every cross section in tube of flow corresponding to incompressible liquid remains constant.
View SolutionA wooden cylinder of length l floats vertically in a liquid of specific gravity ρ with (13)rd part of its length submerged. Another liquid that is immiscible with the previous liquid is poured into it, to just completely submerge the cylinder. If the density of the liquid at the bottom, density of cylinder and density of upper liquid are in G.P., find the fraction of the cylinder submerged in lower liquid.
View SolutionAssertion : Bulk modulus of an incompressible liquid is infinite.
Reason : Compressibility is inverse of bulk modulus.
View Solutionwhen an ideal gas with pressure p and volume V is compressed Isothermally to one - fourth of its volume, is pressure is P1 when the same gas is compressed polytropically according to the equation PV1.5 contents to one - fourth of its initial volume, the pressure is P2 the ratio P1P2 is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,
The density D of the material of the floating cylinder is
View Solution