A closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration a. The resultant normal force by the water on the top of the box.
passes through the centre of top
passes through a point to the righ of the centre
passes through a point to the left of the centre
becomes zero
The correct Answer is:C
To solve the problem of finding the resultant normal force exerted by the water on the top of a closed cubical box that is accelerating horizontally, we can follow these steps:
Step 1: Understand the Setup
We have a closed cubical box filled with water, and the box is accelerating to the right with an acceleration a. The water inside the box will experience forces due to gravity and the acceleration of the box.
Hint: Visualize the box and the water inside it. Consider how the acceleration affects the water's behavior.
Step 2: Identify the Forces Acting on the Water
1. The weight of the water acts downward, which is equal to mg, where m is the mass of the water and g is the acceleration due to gravity.
2. There is a normal force N exerted by the water on the top of the box.
Hint: Remember that the weight of the water acts at the center of mass of the water.
Step 3: Analyze the Effect of Acceleration
Since the box is accelerating to the right, the water will experience a pseudo force acting to the left (due to the non-inertial frame of reference). This pseudo force will cause the water to exert a pressure that is not uniform across the top of the box.
Hint: Consider how the pseudo force affects the pressure distribution in the water.
Step 4: Determine the Pressure Distribution
As the box accelerates, the water will tend to "lag" behind due to inertia, causing a pressure gradient. The pressure will be higher on the left side of the box and lower on the right side.
Hint: Think about how pressure varies in a fluid when it is subjected to an external force.
Step 5: Resultant Normal Force Calculation
The resultant normal force N exerted by the water on the top of the box will not be acting directly downward but will have a component to the left due to the pressure gradient. The resultant normal force can be considered to act at a point to the left of the center of the top surface of the box.
Hint: Visualize the resultant force and its direction concerning the center of the box.
Step 6: Conclusion
Therefore, the resultant normal force by the water on the top of the box acts to the left of the center of the box.
Final Answer: The resultant normal force by the water on the top of the box passes through a point to the left of the center.
---
We have a closed cubical box filled with water, and the box is accelerating to the right with an acceleration a. The water inside the box will experience forces due to gravity and the acceleration of the box.
1. The weight of the water acts downward, which is equal to mg, where m is the mass of the water and g is the acceleration due to gravity.
2. There is a normal force N exerted by the water on the top of the box.
Since the box is accelerating to the right, the water will experience a pseudo force acting to the left (due to the non-inertial frame of reference). This pseudo force will cause the water to exert a pressure that is not uniform across the top of the box.
As the box accelerates, the water will tend to "lag" behind due to inertia, causing a pressure gradient. The pressure will be higher on the left side of the box and lower on the right side.
The resultant normal force N exerted by the water on the top of the box will not be acting directly downward but will have a component to the left due to the pressure gradient. The resultant normal force can be considered to act at a point to the left of the center of the top surface of the box.
Therefore, the resultant normal force by the water on the top of the box acts to the left of the center of the box.
Topper's Solved these Questions
Similar Questions
The pressure at C is
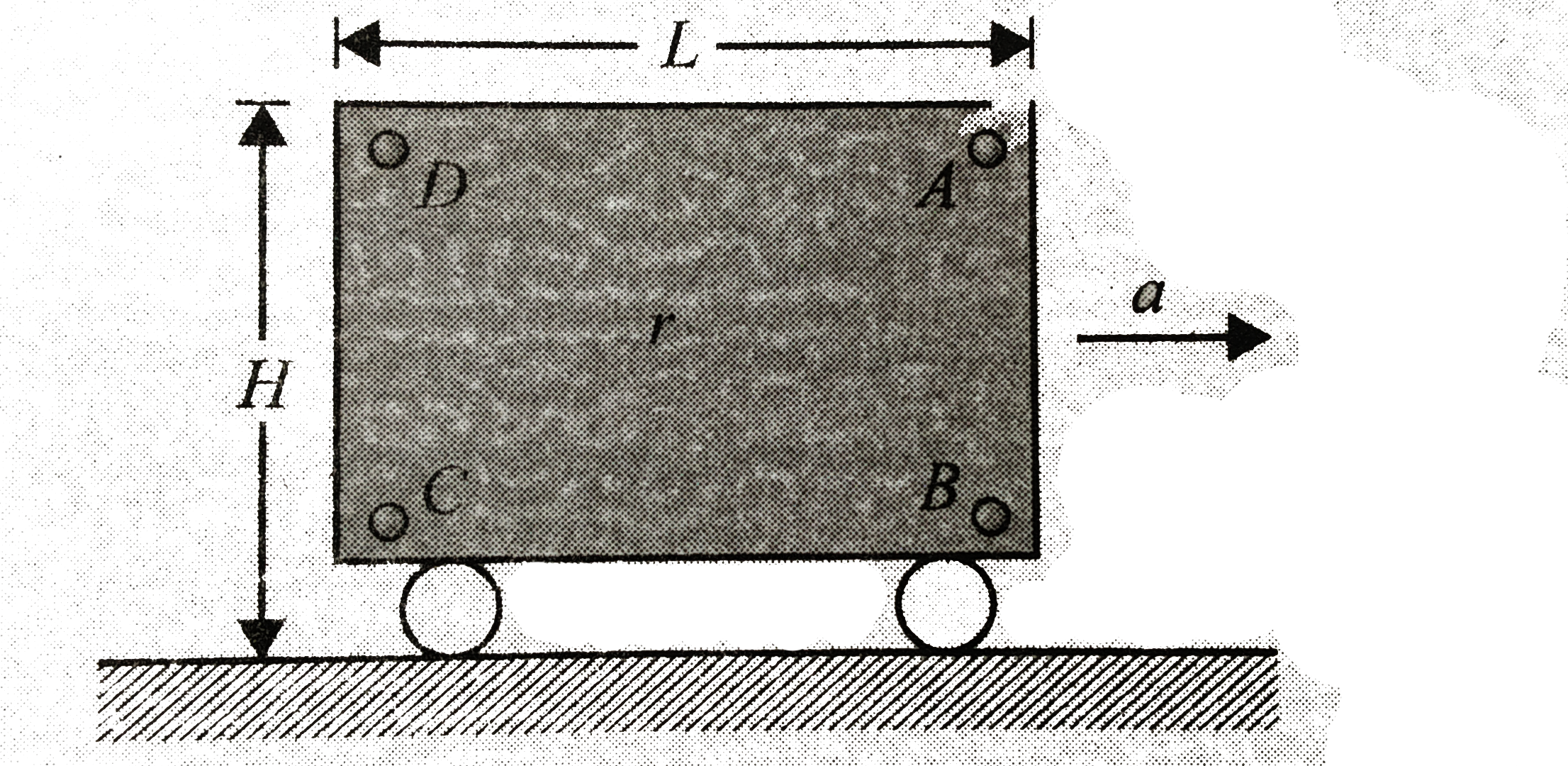
View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
View SolutionA box 'A' is lying on the horizontal floor the compartment of a train running along horizontal ralls from left to right. At time 't', it decelerates. Then the resultant contact force R by the floor on the box is given best by :
View SolutionA beaker filled with water, is accelerated at a rate a ms2 in forward direction. The surface of water shall make an angle
View SolutionWhy a glass bottle completely filled with water and tightly closed at room temperature is likely to burst when kept in the freezer of a refrigerator.
View SolutionAn open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one thrid of volume of water was spilled out. The acceleration was
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
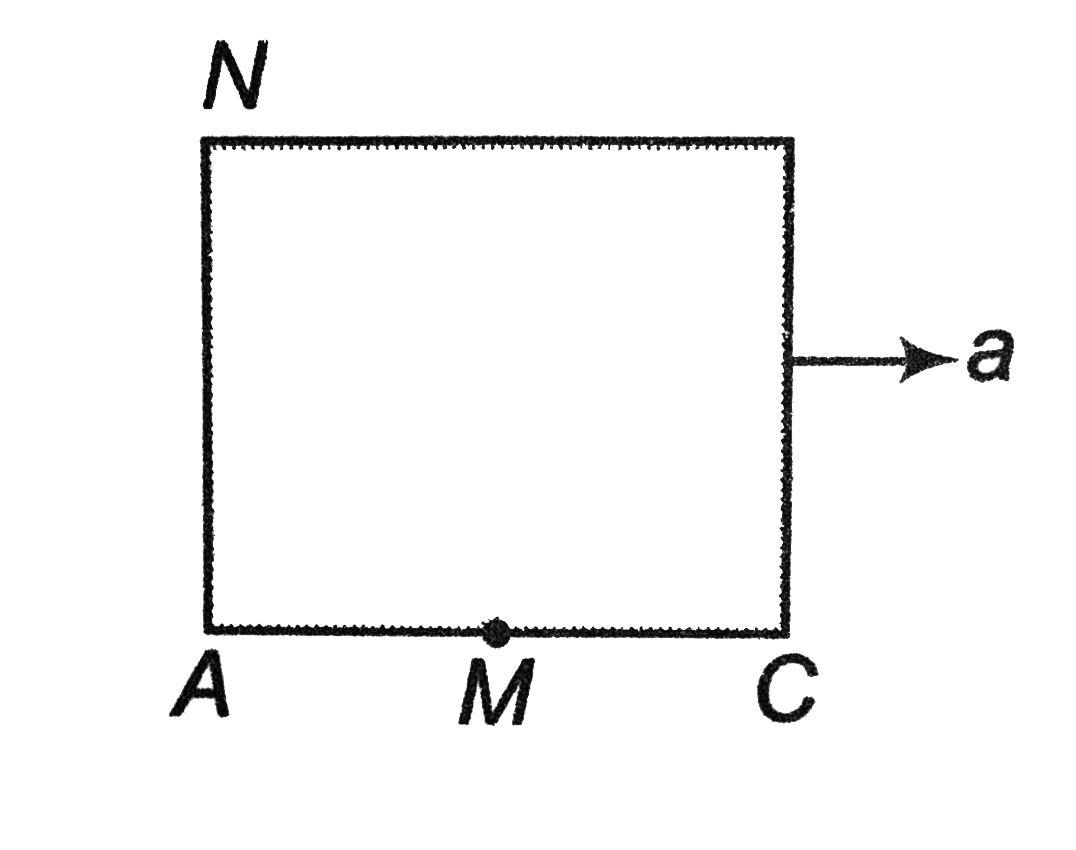
View SolutionA cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
 .
.
View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .

View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
View Solution
