A hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
The correct Answer is:C
To find the density of the material of a hollow spherical body that floats half submerged in water, we can follow these steps:
Step 1: Determine the volumes
First, we need to calculate the volume of the hollow sphere. The volume V of a hollow sphere is given by the formula:
V=43π(R3−r3)
where R is the outer radius and r is the inner radius. In this case, R=8cm and r=6cm.
Calculating the volume:
V=43π(83−63)
=43π(512−216)
=43π(296)
=11843πcm3
Step 2: Calculate the volume of water displaced
Since the sphere is floating half submerged, the volume of water displaced Vd is half of the volume of the hollow sphere:
Vd=12V=12(11843π)=5923πcm3
Step 3: Apply Archimedes' principle
According to Archimedes' principle, the buoyant force Fb acting on the sphere is equal to the weight of the water displaced:
Fb=ρwgVd
where ρw is the density of water (approximately 1000kg/m3) and g is the acceleration due to gravity (approximately 9.81m/s2).
Step 4: Calculate the weight of the hollow sphere
The weight W of the hollow sphere can be expressed as:
W=mg=ρVg
where ρ is the density of the material of the sphere and V is the volume of the hollow sphere calculated earlier.
Step 5: Set the buoyant force equal to the weight
At equilibrium, the buoyant force equals the weight of the sphere:
ρwgVd=ρgV
Cancelling g from both sides, we get:
ρwVd=ρV
Step 6: Solve for the density of the material of the sphere
Rearranging the equation gives:
ρ=ρwVdV
Substituting the values we have:
ρ=1000kg/m3⋅5923πcm311843πcm3
The π and 13 cancel out:
ρ=1000⋅5921184
Calculating this gives:
ρ=5920001184≈500kg/m3
Step 7: Convert to appropriate units
Since we need the density in kg/m3, we can convert cm3 to m3 by noting that 1cm3=10−6m3.
Thus, the density of the material of the sphere is approximately:
ρ≈865kg/m3
Final Answer
The density of the material of the sphere is 865kg/m3.
---
First, we need to calculate the volume of the hollow sphere. The volume V of a hollow sphere is given by the formula:
=43π(512−216)
=43π(296)
=11843πcm3
Since the sphere is floating half submerged, the volume of water displaced Vd is half of the volume of the hollow sphere:
According to Archimedes' principle, the buoyant force Fb acting on the sphere is equal to the weight of the water displaced:
The weight W of the hollow sphere can be expressed as:
At equilibrium, the buoyant force equals the weight of the sphere:
Rearranging the equation gives:
Since we need the density in kg/m3, we can convert cm3 to m3 by noting that 1cm3=10−6m3.
The density of the material of the sphere is 865kg/m3.
Topper's Solved these Questions
Similar Questions
In a conducting hollow sphere of inner and outer radii 5 cm and 10 cm, respectively, a point charge 1 C is placed at point A, that is 3 cm from the center C of the hollow sphere. An external uniform electric field to magnitude 20NC−1 is also applied. Net electric force on this charge is 15 N, away from the center of the sphere as shown. Find the magnitude of net force exerted on the charge placed at point A by the induced charges on the sphere
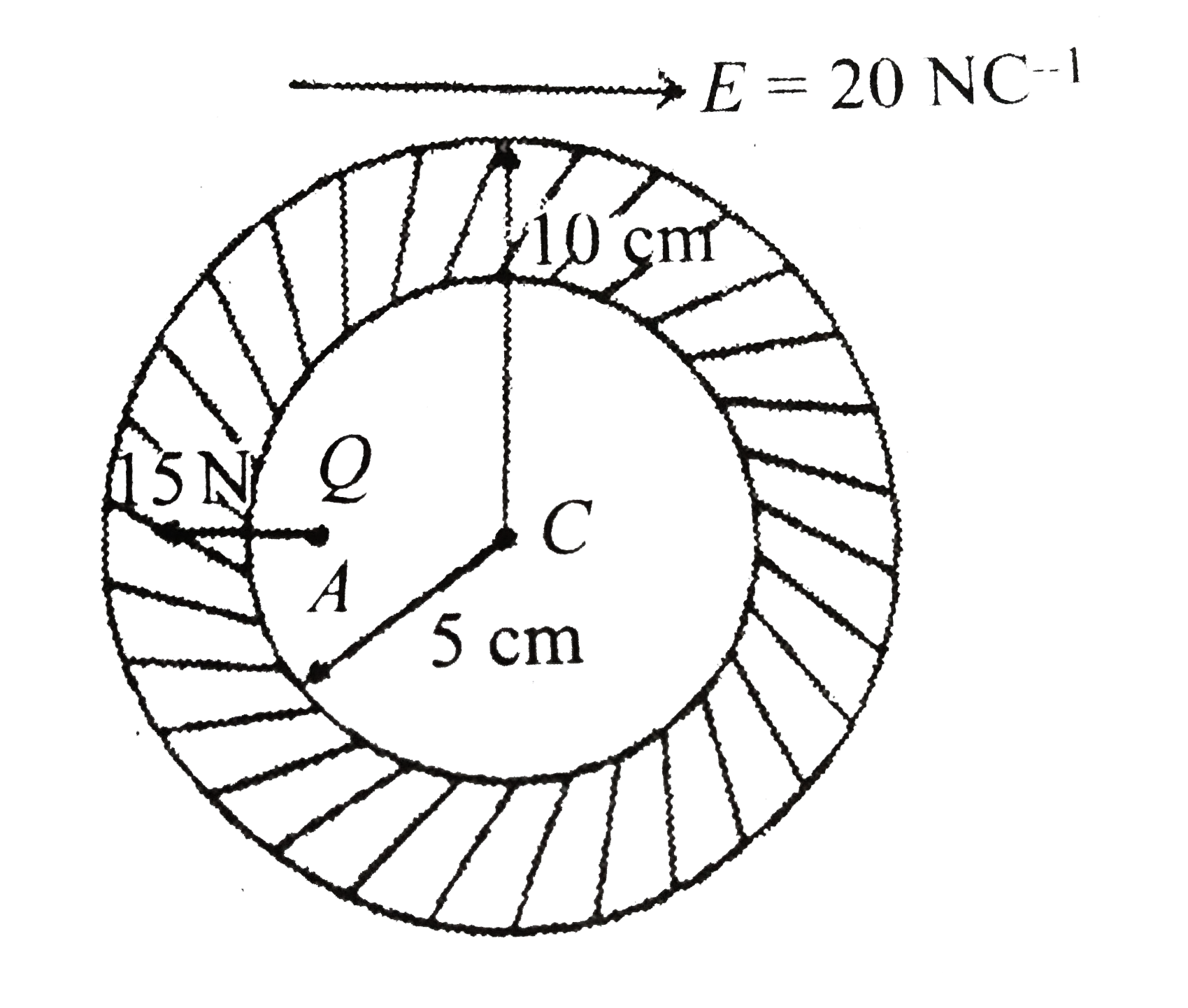 View Solution
View SolutionA small filament is at the centre of a hollow glass sphere of inner and outer radii 8 cm and 9 cm respectively. The refractive index of glass is 1.50. Calculate the position of the image of the filament when viewed from outside the sphere.
View SolutionA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
View SolutionA hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
View SolutionA hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
View SolutionA hollow metallic sphere has inner and outer radii, respectively as 5 cm and 10 cm if the mass of the sphere is 2.5 kg, find (a) density of the material, (b) relative density of the material of the sphere.
View SolutionA hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
View SolutionA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View SolutionMetallic spheres of radii 6 cm, 8 cm and 10 cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
View Solution

