A U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
The correct Answer is:A
To solve the problem of finding the difference in heights of the liquid in the two arms of a U-tube that is being accelerated horizontally, we can follow these steps:
Step 1: Understand the setup
We have a U-tube containing a liquid, and the entire U-tube is being accelerated horizontally with a constant acceleration a0. This acceleration will affect the pressure distribution in the liquid.
Step 2: Define the pressure difference
Let h be the difference in height of the liquid in the two arms of the U-tube. The pressure difference between the two arms due to this height difference can be expressed using the hydrostatic pressure formula:
P1−P2=ρgh
where:
- P1 is the pressure at the bottom of the higher liquid column,
- P2 is the pressure at the bottom of the lower liquid column,
- ρ is the density of the liquid,
- g is the acceleration due to gravity.
Step 3: Consider the effect of acceleration
When the U-tube is accelerated with an acceleration a0, there is an additional pressure difference created due to the horizontal acceleration. This pressure difference can be expressed as:
P1−P2=ρLa0
where L is the horizontal separation between the two vertical limbs of the U-tube.
Step 4: Set the two pressure differences equal
Since both expressions represent the same pressure difference, we can set them equal to each other:
ρgh=ρLa0
Step 5: Simplify the equation
We can cancel ρ from both sides of the equation (assuming the density is constant and non-zero):
gh=La0
Step 6: Solve for the height difference h
Now, we can solve for h:
h=La0g
Final Result
Thus, the difference in the heights of the liquid in the two arms of the U-tube is given by:
h=La0g
---
We have a U-tube containing a liquid, and the entire U-tube is being accelerated horizontally with a constant acceleration a0. This acceleration will affect the pressure distribution in the liquid.
Let h be the difference in height of the liquid in the two arms of the U-tube. The pressure difference between the two arms due to this height difference can be expressed using the hydrostatic pressure formula:
P1−P2=ρgh
where:
- P1 is the pressure at the bottom of the higher liquid column,
- P2 is the pressure at the bottom of the lower liquid column,
- ρ is the density of the liquid,
- g is the acceleration due to gravity.
When the U-tube is accelerated with an acceleration a0, there is an additional pressure difference created due to the horizontal acceleration. This pressure difference can be expressed as:
P1−P2=ρLa0
where L is the horizontal separation between the two vertical limbs of the U-tube.
Since both expressions represent the same pressure difference, we can set them equal to each other:
ρgh=ρLa0
We can cancel ρ from both sides of the equation (assuming the density is constant and non-zero):
gh=La0
Now, we can solve for h:
h=La0g
Thus, the difference in the heights of the liquid in the two arms of the U-tube is given by:
h=La0g
Topper's Solved these Questions
Similar Questions
A container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.
 View Solution
View SolutionA container containing a liquid is moving down an incline plane with constant acceleration 'a' . The angle made by the water surface in equilibrium with the inclined plane is
 View Solution
View SolutionA liquid can rise to a height of h in a capillary tube of length l (l>h). The tube filled with the liquid is kept horizontal with its two ends open. Now the tube is kept vertical with the liquid in it. Some liquid flows out. Find the height of the liquid remaining in the tube if the surface tension of the liquid is σ.
View SolutionA bent tube of uniform cross section is mounted on a cart which is accelerating towards right with constant acceleration 'a'. The total length of the liquid is 2√2l. Find the level difference between two limbs in equilibrium (a=2m/s2,l=10m)
 View Solution
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isView SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
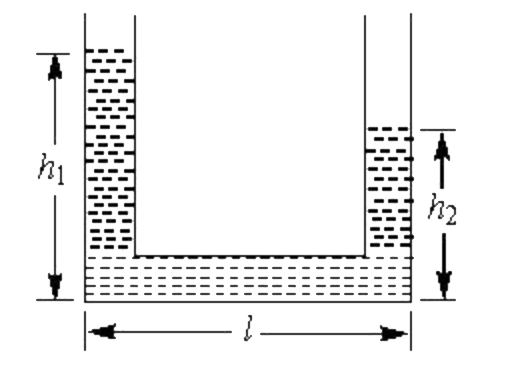 View Solution
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
 View Solution
View SolutionAn open vessel containing liquid is moving with constant acceleration a on a levelled horizontal surface. For this situation mark out the correct statement(s).
 View Solution
View SolutionTwo vertical glass tibes filled with a liquid are connected at their lower ends by a horizontal capillary tube. One tube is surrounded by a bath containing ice and water at 0∘C and the other by hot water a t∘C. The difference in the height of the liquid in the two columns is Δh, and the height of the colume at 0∘C is h0. coefficient of volume expansion of the liquid is.
 View Solution
View Solution

