When a block of mass M is suspended by a long wire of length L, the elastic potential energy stored in the wire is 12×stress×strain×volume. Show that it is equal to 12Mgl where l is the extension. The loss in gravitational potential energy of the mass earth system is Mgl. Where does the remaining 12Mgl energy go ?
To solve the problem, we need to show that the elastic potential energy stored in the wire when a block of mass M is suspended by it is equal to 12Mgl, where l is the extension of the wire. We also need to analyze where the remaining energy goes when the gravitational potential energy loss is MgL.
1. Identify the Gravitational Potential Energy Loss:
When the block of mass M is suspended, it falls a distance L. The loss in gravitational potential energy (GPE) can be calculated using the formula:
GPE=MgL
2. Define Elastic Potential Energy:
The elastic potential energy (EPE) stored in the wire can be expressed as:
EPE=12×Stress×Strain×Volume
3. Calculate Stress and Strain:
- Stress is defined as the force per unit area:
Stress=FA=MgA
- Strain is defined as the change in length per original length:
Strain=lL
4. Calculate the Volume of the Wire:
The volume V of the wire can be expressed as:
V=A×L
5. Substituting Values into EPE:
Now substituting the values of stress, strain, and volume into the EPE formula:
EPE=12×(MgA)×(lL)×(A×L)
Simplifying this expression:
EPE=12×Mg×lL×L=12Mgl
6. Comparison of Energies:
We have shown that the elastic potential energy stored in the wire is:
EPE=12Mgl
The total gravitational potential energy lost is:
GPE=MgL
7. Energy Accounting:
The difference between the gravitational potential energy lost and the elastic potential energy stored is:
Energy lost=GPE−EPE=MgL−12Mgl
This simplifies to:
Energy lost=12MgL
8. Conclusion on Energy Loss:
The remaining energy, which is 12MgL, is converted into heat due to internal friction and other dissipative processes in the wire.
Final Answer:
The elastic potential energy stored in the wire is 12Mgl, and the remaining 12MgL energy is converted into heat.
When the block of mass M is suspended, it falls a distance L. The loss in gravitational potential energy (GPE) can be calculated using the formula:
GPE=MgL
The elastic potential energy (EPE) stored in the wire can be expressed as:
EPE=12×Stress×Strain×Volume
- Stress is defined as the force per unit area:
Stress=FA=MgA
- Strain is defined as the change in length per original length:
Strain=lL
The volume V of the wire can be expressed as:
V=A×L
Now substituting the values of stress, strain, and volume into the EPE formula:
EPE=12×(MgA)×(lL)×(A×L)
Simplifying this expression:
EPE=12×Mg×lL×L=12Mgl
We have shown that the elastic potential energy stored in the wire is:
EPE=12Mgl
The total gravitational potential energy lost is:
GPE=MgL
The difference between the gravitational potential energy lost and the elastic potential energy stored is:
Energy lost=GPE−EPE=MgL−12Mgl
This simplifies to:
Energy lost=12MgL
The remaining energy, which is 12MgL, is converted into heat due to internal friction and other dissipative processes in the wire.
The elastic potential energy stored in the wire is 12Mgl, and the remaining 12MgL energy is converted into heat.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SOUND WAVESBOOK - HC VERMA ENGLISHCHAPTER - SOUND WAVESEXERCISE - All Questions
133 Videos
Similar Questions
When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L+l). The elastic potential energy stored in the extended wire is
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solutionwhen a metal wire elongates by hanging a load Mg on it , the gravitational poyential energy of mass M decreases by Mgl. This energy appears
View SolutionWhen a force of 80 N is applied on a uniform steel wire, its free end elongates by 1.2 mm. Find the energy stored in the wire.
View SolutionTwo bodies of equal masses are placed at heights and 2h. Find the ratio of their gravitational potential energies
View SolutionA body of mass M is attached to lower end of a metal wire whose upper End is fixed. The elongation is l. The ratio of loss of gravitational potential energy to the energy stored in the wire is
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
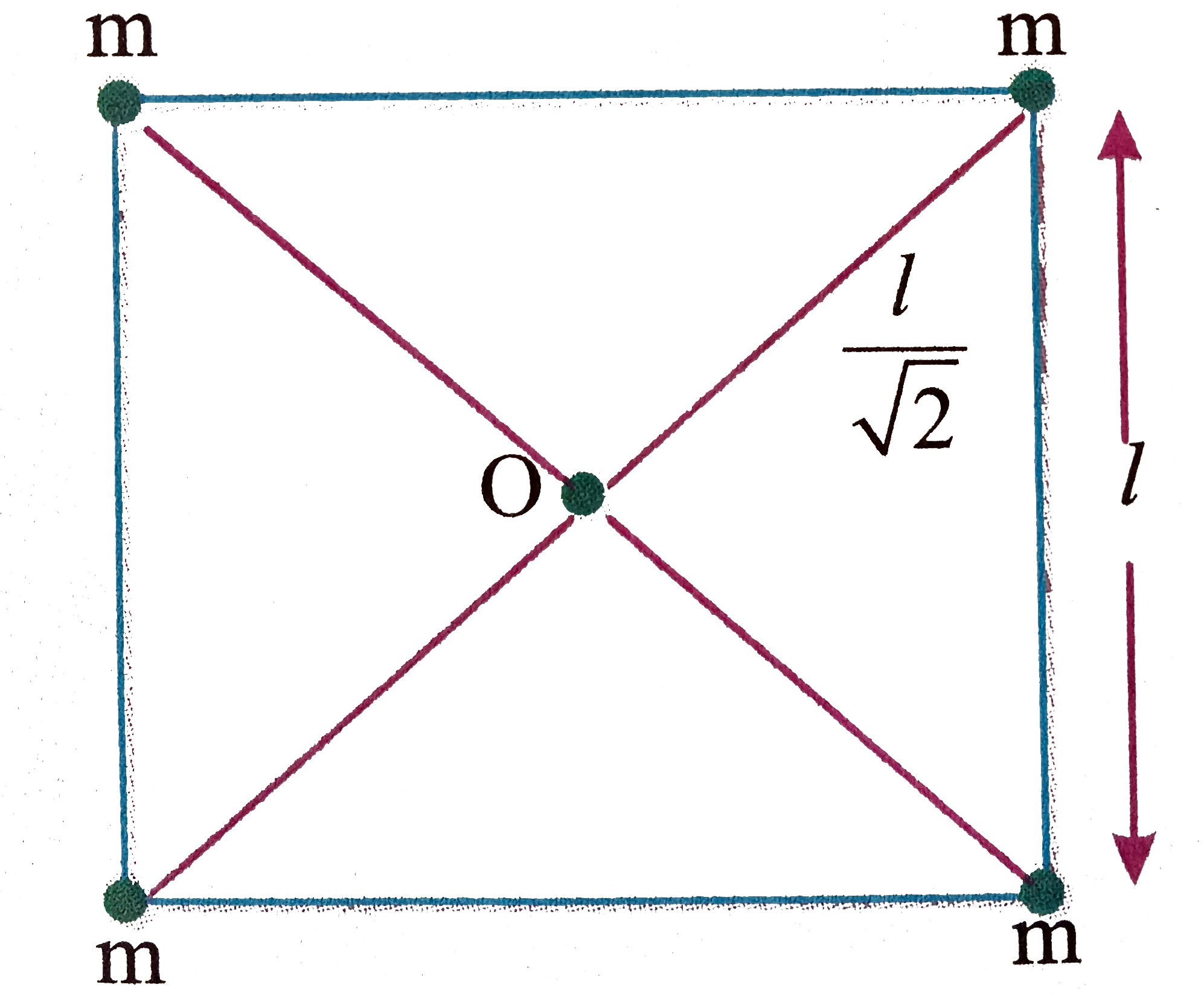
View SolutionA body of mass m is placed on the earth's surface . It is taken from the earth's surface to a height h = 3 R where R is the radius of the earth. The change in gravitational potential energy of the body is
View SolutionThe height from the surface of earth at which the gravitational potential energy of a ball of mass m is half of that at the centre of earth is (where R is the radius of earth)
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View Solution
