A body of mass M is attached to lower end of a metal wire whose upper End is fixed. The elongation is l. The ratio of loss of gravitational potential energy to the energy stored in the wire is
1
2
12
43
The correct Answer is:B
To solve the problem step by step, we will analyze the loss of gravitational potential energy and the energy stored in the wire due to elongation.
Step 1: Understand the Setup
A body of mass M is attached to the lower end of a metal wire, which is fixed at the upper end. When the mass is attached, the wire elongates by a length l.
Step 2: Calculate the Loss of Gravitational Potential Energy
Initially, the mass is at a height h. After elongation, the height of the mass becomes h−l. The loss in gravitational potential energy (ΔPE) can be calculated as:
ΔPE=Initial PE−Final PE=Mgh−Mg(h−l)=Mgh−Mgh+Mgl=MgL
Step 3: Calculate the Energy Stored in the Wire
The energy stored in the wire due to elongation can be calculated using the formula for elastic potential energy:
Es=12×Force×Elongation
The force exerted on the wire is equal to the weight of the mass, which is Mg. Therefore, the energy stored in the wire is:
Es=12×Mg×l=Mgl2
Step 4: Calculate the Ratio of Loss of Gravitational Potential Energy to Energy Stored in the Wire
Now, we need to find the ratio of the loss of gravitational potential energy to the energy stored in the wire:
Ratio=ΔPEEs=MgLMgl2=MgL⋅2Mgl=2Ll=2
Final Answer
The ratio of the loss of gravitational potential energy to the energy stored in the wire is:
Ratio=2
---
A body of mass M is attached to the lower end of a metal wire, which is fixed at the upper end. When the mass is attached, the wire elongates by a length l.
Initially, the mass is at a height h. After elongation, the height of the mass becomes h−l. The loss in gravitational potential energy (ΔPE) can be calculated as:
ΔPE=Initial PE−Final PE=Mgh−Mg(h−l)=Mgh−Mgh+Mgl=MgL
The energy stored in the wire due to elongation can be calculated using the formula for elastic potential energy:
Es=12×Force×Elongation
The force exerted on the wire is equal to the weight of the mass, which is Mg. Therefore, the energy stored in the wire is:
Es=12×Mg×l=Mgl2
Now, we need to find the ratio of the loss of gravitational potential energy to the energy stored in the wire:
Ratio=ΔPEEs=MgLMgl2=MgL⋅2Mgl=2Ll=2
The ratio of the loss of gravitational potential energy to the energy stored in the wire is:
Ratio=2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - C)
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - D)
Explore 3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - A)
Explore 31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- Mock test 03Book:AAKASH INSTITUTE ENGLISHChapter:Mock test 03Exercise:EXAMPLE
Explore 44 Videos
Similar Questions
A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View SolutionWhen a metal wire elongates by hanging a load on it, the gravitational potential energy is decreased.
View SolutionA ball of mass m is attached to the lower end of a vertical string whose upper end is fixed. An identcial ball 'B' moving with a velocity v0=6m/s at an angle θ=45∘ from vertical collides elastically with the ball 'A' as shown.
The verocity of the ball 'B' just after collision is
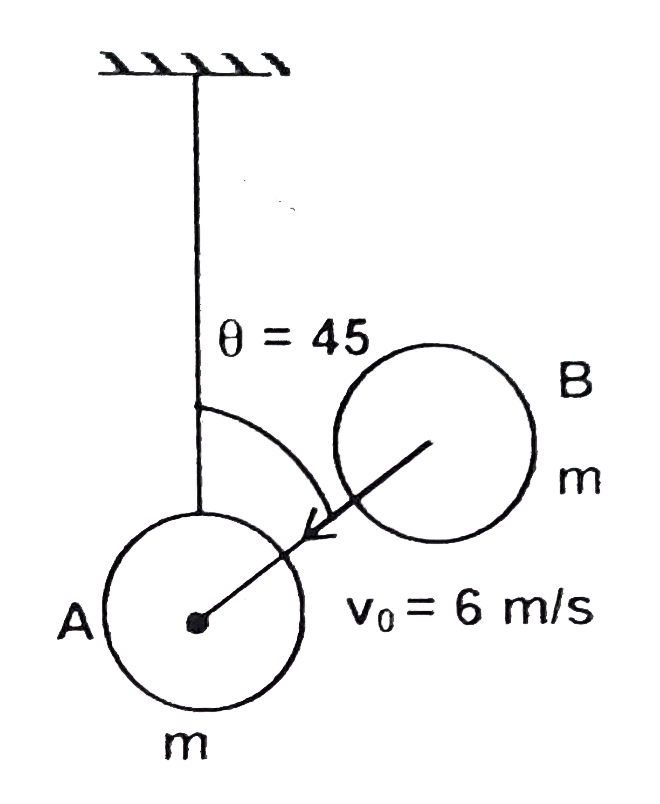
View SolutionTwo bodies of equal masses are placed at heights and 2h. Find the ratio of their gravitational potential energies
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View Solutionwhen a metal wire elongates by hanging a load Mg on it , the gravitational poyential energy of mass M decreases by Mgl. This energy appears
View SolutionOne end of an unstretched vertical spring is attached to the ceiling and an object attached to the other end is slowly lowered to its equilibrium position. If S is the gain in spring energy and G is the loss in gravitational potential energy in the process, then
View SolutionA wire 3m long and diameter 0.3 mm is stretched by a load of 2kg. If the elongation is 2mm, find the Young.s modulus of the material of the wire and the potential energy stored in the wire.
View SolutionA body is attached to a spring whose other end is fixed. If the spring is elongated by x, its potential energy is U=5x2, where x is in metre and U is in joule. U-x graph is
View Solution