The equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
The correct Answer is:A, B, C, D
Given y=Ae−(xa+tT)2
a. [A]=[M0L1T0]
[T]=[M^0L^0T^-1]<br>[a]=[M0L1T0]
b. Wave speed v=lamda/T=a/T[Here lamda=a]<br>c.Ify=f(t+x/v)<br>→wavetravell∈g∈¬ativedirectionandify=f(t-x/v)<br>→wavetravell∈gpositivedirectio∈<br>So,y=Ae−[(xa)+(tT)]2
=Ae−1T[T+(xTa)]2
=Ae−1T[t+xV]
=Ae−f[t+xV]
Hence wave travelling is negative direction
d. Wave speed ltbr> V=at
Maximum pusle at t=T
is (aT)×T=a (negative x-axis)<br>Maξμmpuseatt=2T=(a/Txx2T)<br>=2a
(along negative x-axis)
so the wave travelling in negative x direction.
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -2
9 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
Similar Questions
The equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionThe equation of a wave travelling on a string is given by Y(mn) = 8 sin[(5m−1x−(4s−1t]. Then
View Solution
Knowledge Check
The equation of a wave travelling in a string can be written as y=3cosπ(10t−x). Its wavelength is
A100 cmB2 cmC5 cmDnone of the above
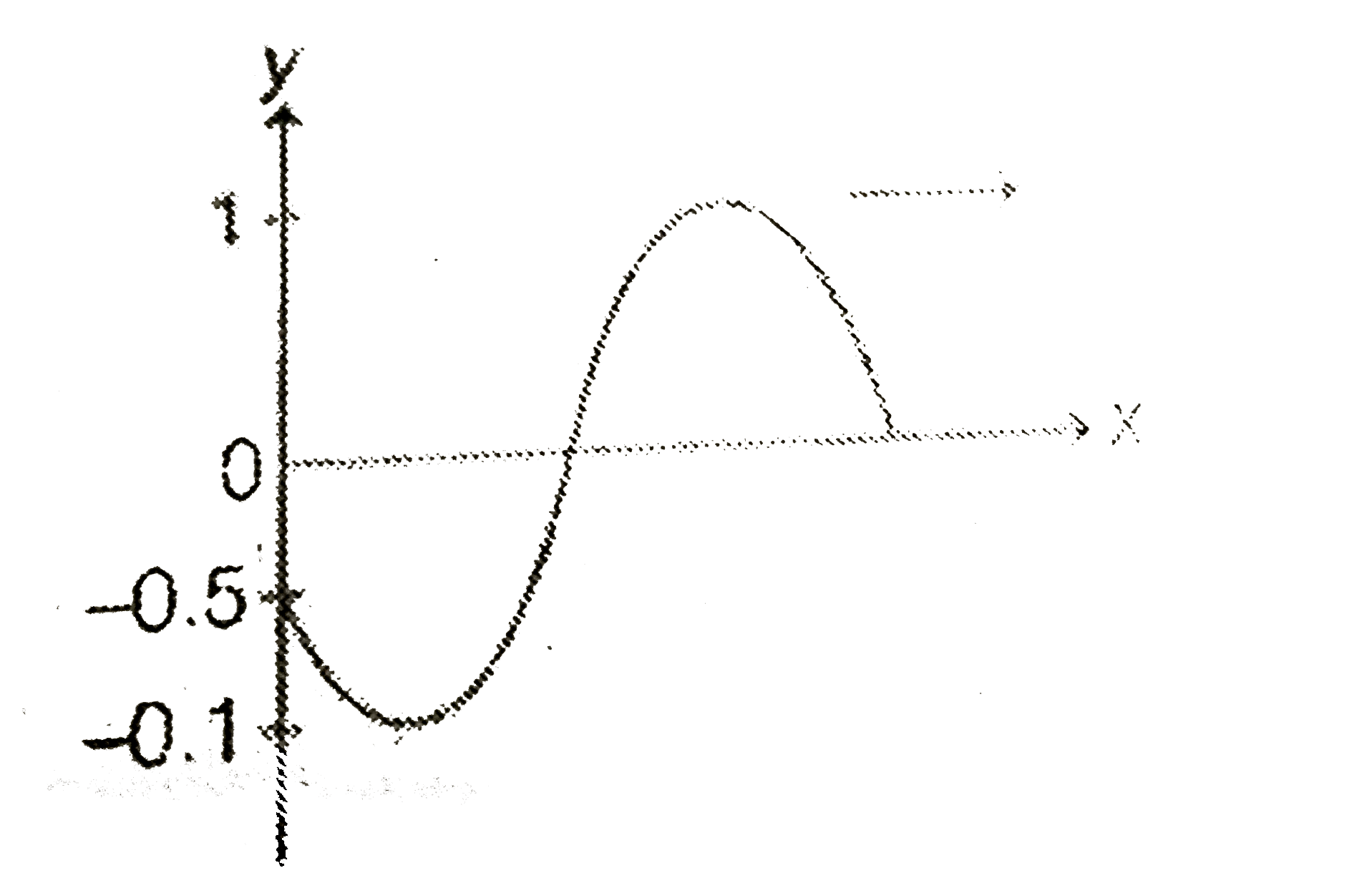
The equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
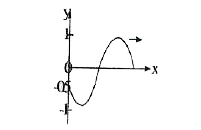
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
View SolutionThe equation of a wave travelling on a string given by, y=γe−((xα+tβ)2)what will be speed of of wave?
View SolutionA travelling wave on a long stretched string along the positIve x-axis is given by y=5mme(t5s−x5cm)2. Using this equation answer the following questions.
At t = 0, x = 0, the displacement of the wave is
View SolutionA travelling wave on a long stretched string along the positIve x-axis is given by y=5mme(T5s−x5cm)2 . Using this equation answer the following questions.
The velocity of the wave is
View SolutionA transverse wave travelling on a stretched string is is represented by the equation
y=2(2x−6.2t)2+20. Then ,
View SolutionThe equetion of a wave travelling on a string is
y=4sin(π)2(8t−x8)
if x and y are in centimetres, then velocity of waves is
View Solution
