Three observers A, B and C measure the speed of light coming from a source to be vA,vB and vC. The observer A moves towards the source and C moves away from the soure at the same speed. The observer B stays stationary. The surrounding space is vacuum everywhere .
υA>υB>υC
υA<υB<υC
υA=υB=υC
υB=12(upslionA+υc).
The correct Answer is:C, D
To solve the problem, we need to analyze the situation involving the three observers A, B, and C, and their measurements of the speed of light.
1. Understanding the Situation:
- Observer A is moving towards the light source.
- Observer C is moving away from the light source.
- Observer B is stationary.
- The speed of light in a vacuum is denoted as c.
2. Applying the Principle of Relativity:
- According to Einstein's theory of relativity, the speed of light in a vacuum is constant and is the same for all observers, regardless of their motion relative to the light source.
- Therefore, the speed of light measured by each observer should be the same.
3. Setting Up the Equations:
- Let vA be the speed of light measured by observer A, vB by observer B, and vC by observer C.
- Based on the principle of relativity, we can write:
vA=vB=vC=c
4. Analyzing the Observers' Movements:
- Observer A, moving towards the source, might intuitively seem to measure a higher speed of light, but according to relativity, this is not the case.
- Observer C, moving away from the source, might seem to measure a lower speed of light, but again, relativity dictates that the speed remains c.
5. Conclusion:
- Therefore, we conclude that:
vA=vB=vC=c
- This means that all observers measure the speed of light as c, regardless of their motion.
Final Answer:
The relationship between the velocities measured by the three observers is:
vA=vB=vC=c
- Observer A is moving towards the light source.
- Observer C is moving away from the light source.
- Observer B is stationary.
- The speed of light in a vacuum is denoted as c.
- According to Einstein's theory of relativity, the speed of light in a vacuum is constant and is the same for all observers, regardless of their motion relative to the light source.
- Therefore, the speed of light measured by each observer should be the same.
- Let vA be the speed of light measured by observer A, vB by observer B, and vC by observer C.
- Based on the principle of relativity, we can write:
vA=vB=vC=c
- Observer A, moving towards the source, might intuitively seem to measure a higher speed of light, but according to relativity, this is not the case.
- Observer C, moving away from the source, might seem to measure a lower speed of light, but again, relativity dictates that the speed remains c.
- Therefore, we conclude that:
vA=vB=vC=c
- This means that all observers measure the speed of light as c, regardless of their motion.
The relationship between the velocities measured by the three observers is:
vA=vB=vC=c
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Exercises41videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -117videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
Similar Questions
Block A is moving away from the wall at a speed v and acceleration a.
 View Solution
View Solutionif the speed of a sound source is equal to the speed fo sound and the source is moving away from the observer, then the ratio of apparent frequency to the original frequency is
View SolutionAn observer measures speed of light to be C, when he is stationary with respect to the source. If the observer moves with velocity V towards the source then the velocity of light observed will be
View SolutionAn observer approaches towards a stationary source of sound at constant velocity and recedes away at the same speed. The graph of wavelength observed with time is:
View SolutionAn observer A is moving directly towards a stationary sound source while another observer B is moving away from the source with the same velocity. Which of the following statements are correct?
View SolutionA source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View SolutionA fixed source of sound emitting a certain frequency appears as fa when the observer is apporoaching the source with υ0 and fr when the observer recedes from the source with the same speed. The frequency of source is
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
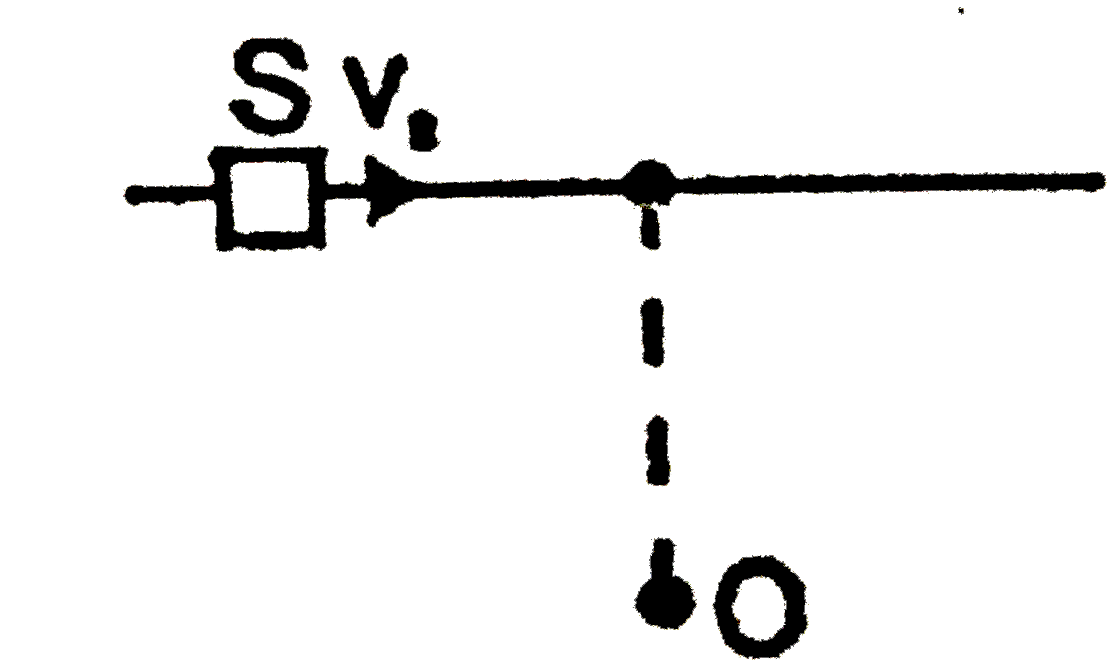 View Solution
View SolutionAn observer moves on the same line on which two sources of sound of frequency 660Hz are present. The observer observes beat frequency of 10Hz. If speed of sound is 300m/s then speed of the observer is:
View SolutionWhen a loop moves towards a stationary magnet with speed v, the induced emf in the loop is E. If the magnet also moves away from the lop with the same speed, then the emf inducted in the loop is
View Solution

