A long narrow horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit, Find the fringe-width if the light used has a wavelength of 700 nm.
The correct Answer is:C
Givent that D=1m
λ=700mm=700×10−3m<br>Sincea=1mm<br>d=2a=2mm<br>=2xx10^-3m<br>[Lloyd'smirrorexperiment]
Fringe width =(lamdaD)/d<br>=(700xx10^9xx1m)/(2xx0^-3m)<br>0.35mm
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -210videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
Similar Questions
A long horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and the after reflection is seen on a screen 1 m away from the slit. If the mirror reflects only 64% of the light falling on it, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is
View SolutionA long narrow horizontal slit lies 1mm above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen ∑ distance 1m from the slit. The wavelength of light is 600nm. Then the distance of the first maxima above the mirror is equal to (d<<D) :
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
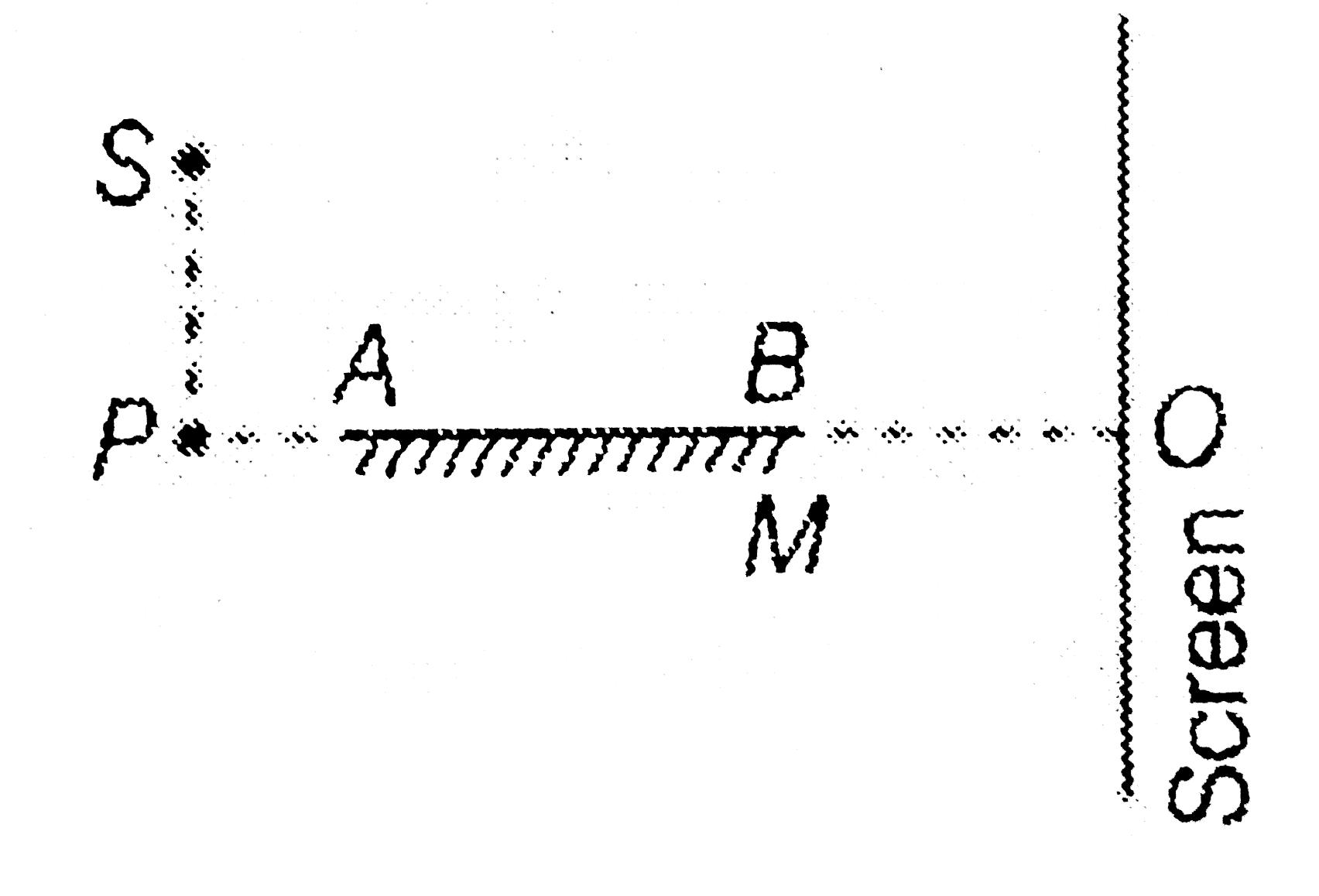
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?View SolutionA narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
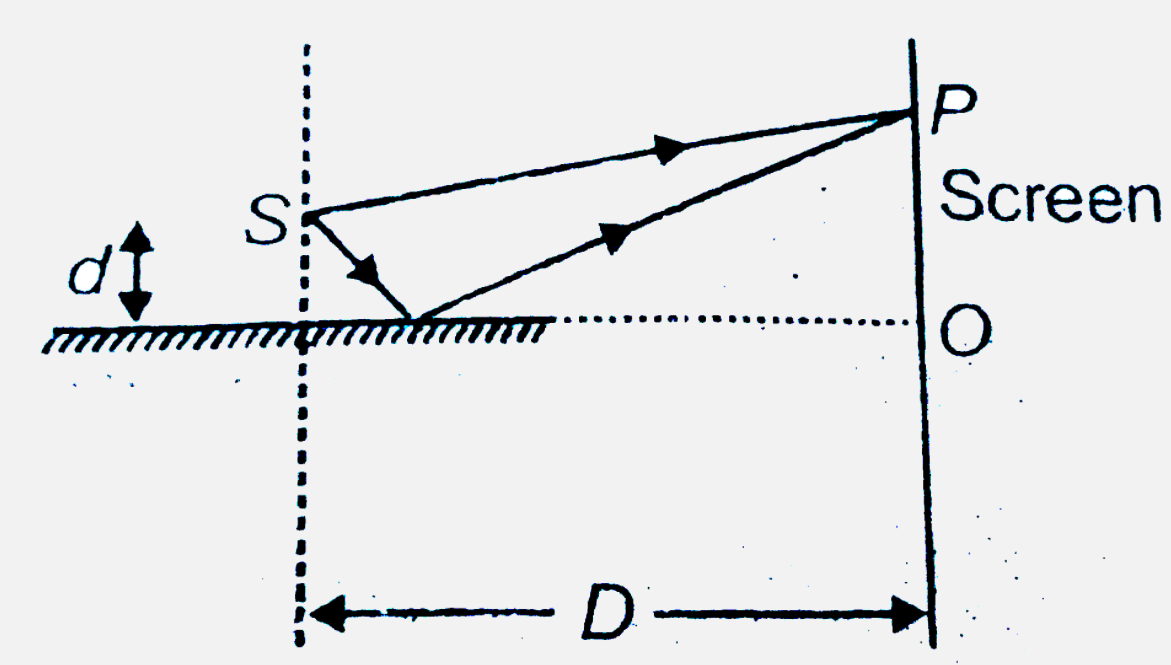
View SolutionA narrow slit S transmitting light of wavelength 'λ'. Is placed at a distance d above a large plane mirror as shown. The light coming directly from the slit and that coming after the reflection interfere at a screen S placed at a distance D from the slit. at what distance from point O, the resultant intensity is maximum ? (there is a phase change of π of reflection from the mirror)
View SolutionTwo slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View SolutionTwo slits in YDSE are placed 2 millimeter from each other. Interference pattern is observed on a screen placed 2 m from the plane of slits. What is the fringe width for a light of wavelength 400 nm?
View SolutionThe distace between the first and the sixth minima in the diffraction pattern of a single slit is 0.5mm. The screen is 0.5m away from the slit. If wavelength of the light used is 5000A0, then the slit width will be
View SolutionTwo slits in Young's double slits experiment are spaced 0.1 millimeter apart. If the fringe width is obtained as 5 mm on screen 1.5m away from slits. Find the wavelength of the light used.
View SolutionIn Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
View Solution