A narrow beam of light passes through a slab obliquely and is then received by an eye. The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation.

Step by step video & image solution for A narrow beam of light passes through a slab obliquely and is then received by an eye. The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ray of light passes through two slabs of same thickness. In the first slab n1 waves are formed and in the second slab n2. Find refractive <br> index of second medium with respect to first.
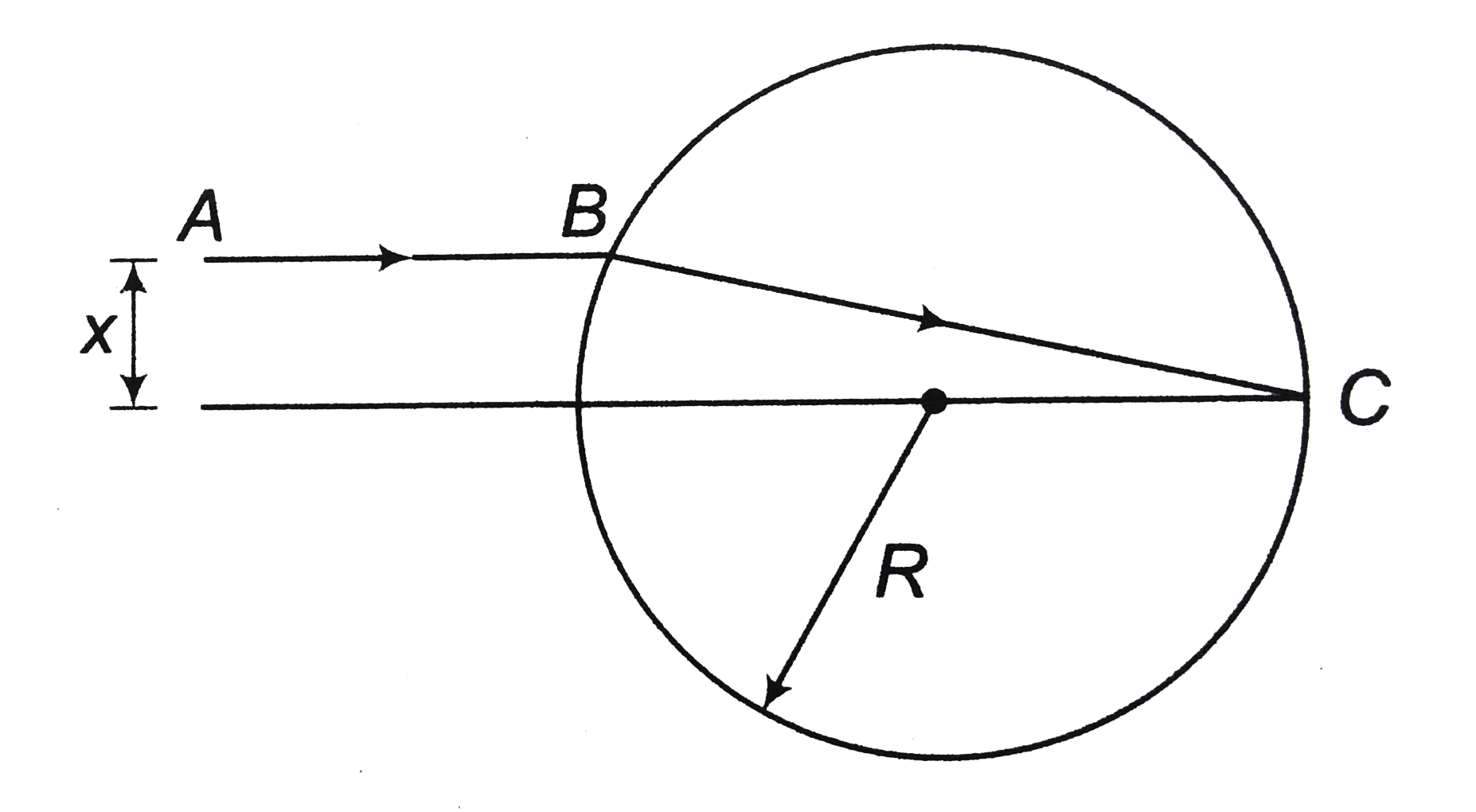
View SolutionA spherical ball of transparent material has index of refractionμ. A narrow beam of light AB is aimed as shown. What must the index of refraction be in order that the light is focused at the point C on the opposite end of the diameter from where the light entered? Given that x>>R.
View SolutionA ray of light is refracted through a sphere whose material has a refractive index μ in such a way that it passes through the extremities of two radii which make an angle β with each other. Prove that if α is the deviation of the ray caused by its passage through the sphere, then
cos(β−α2)=μcos(βα)
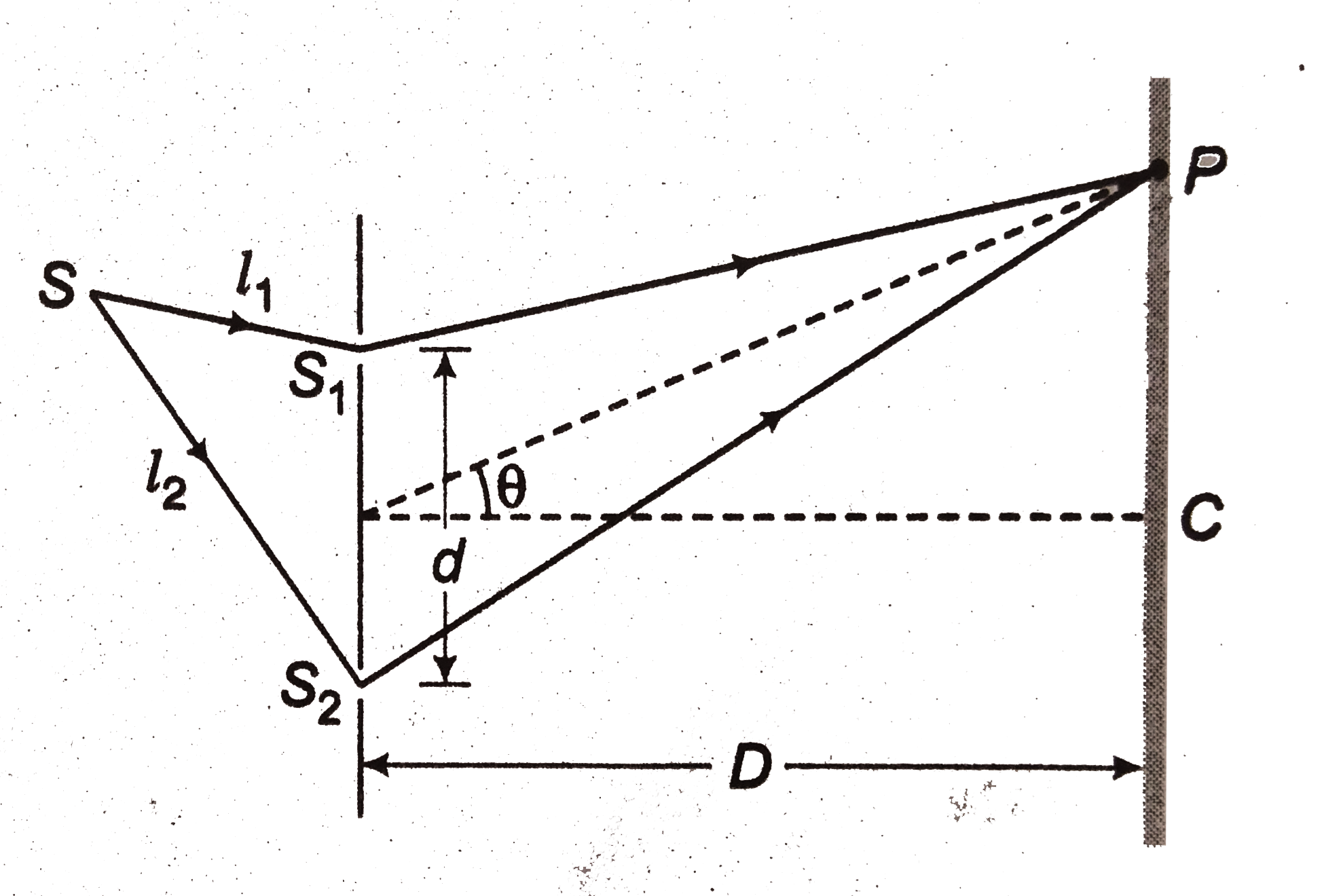
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
View SolutionA glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
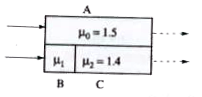
View SolutionA slab of transparent materials is made as shown in the figure. Monochromatic parallel beams of light are normally incident on the slabs. The thickness of C is twice the thickness of B. The number of waves is A= the number of waves in the combination of B and C. The refractive index of material A is μ0=1.5 and that of C is μ2=1.4
View SolutionWhen a light wave passes from a rarer medium to a denser medium, there will be a phase change of π radians. This difference brings change in the conditions for constructive and destructive interference. This phenomena also reasons the fromation of interference pattern in thin films like, oily layer, soap film, etc., but has no reason on the shifting of fringes from the central portion outward. The shift is dependent on the refractive index of the material as per the relation, Δy=(μ−1)t
On introducing a transparent slab (μ) the central fringe shifts to the point originally occupied by the fifth bright fringe. The thickness of the slab is
View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum).
if c is the velocity of light in a vacuum the velocity in a medium of refractive index μ is cμ hence time taken to travel a distance l is μlc if the light passes through a number of media, the total time taken is (1c)∑μl or 1c∫μdl if refractive index varies continuously. Now ∑μl is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction.
Q. If refractive index of a slab varies as μ=1+x2 where x is measured from one end then optical path length of a slab of thickness 1 m is
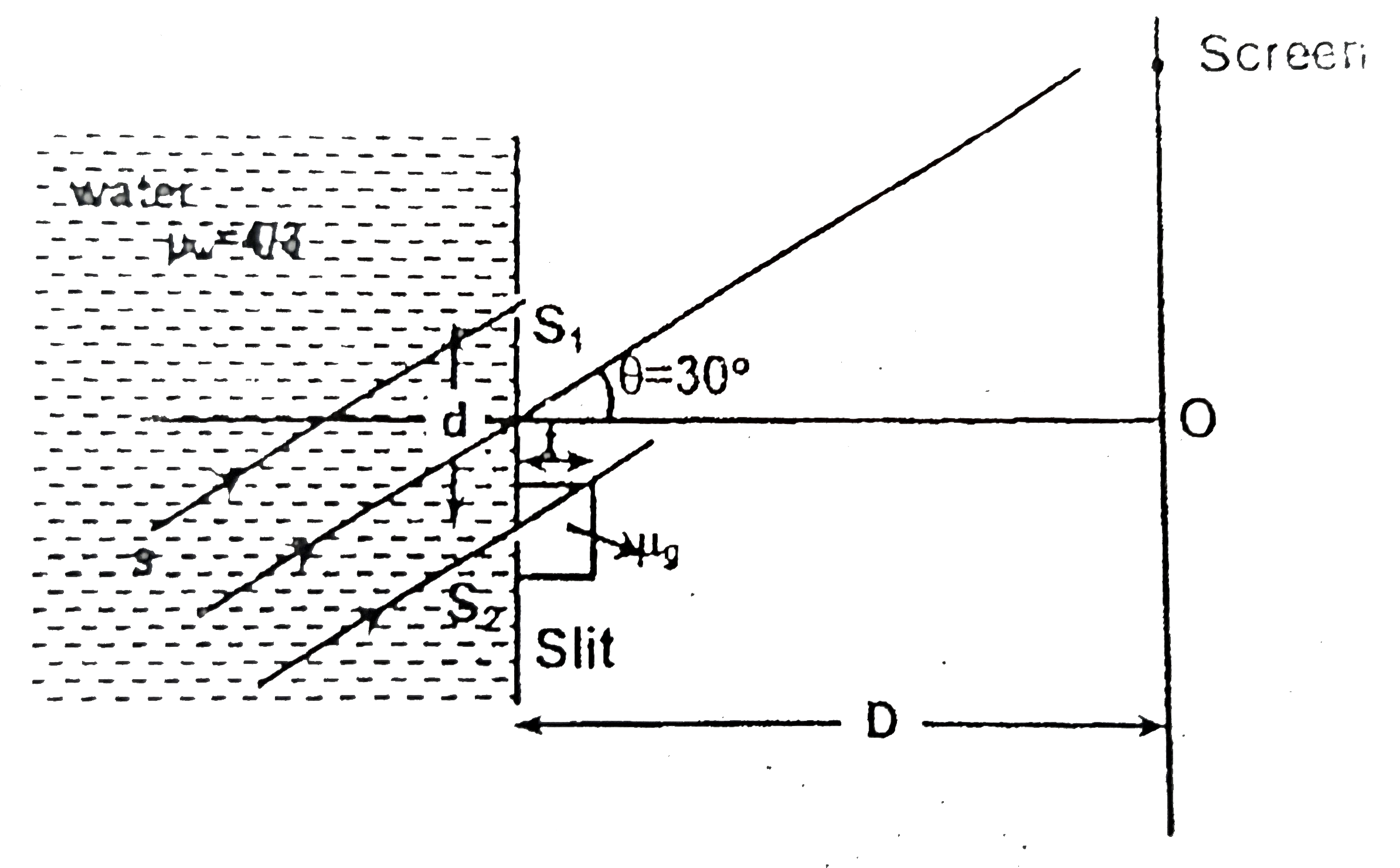
View SolutionIn a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
View SolutionTwo transparent slabs have the same thickness as shown in figure. One in made of material A of refractive index 1.5. The other is made of two materilas B and C with thickness in the ratio 1:2. The refractive index of C is 1.6. If a monochromatic parallel beam passing through the slabs has the same number of wavelengths inside both, the refractive index of B is
View Solution
