A slide projector has to project a 35 mm slide (35mm×23mm) on a 2 m xx 2m screen at a distance of 10 m from the lens. What should be the focal length of the lens in the projector ?
The correct Answer is:A, B, C
To find the focal length of the lens in the projector, we can follow these steps:
Step 1: Understand the problem
We need to project a 35 mm x 23 mm slide onto a 2 m x 2 m screen, with the lens positioned 10 m away from the screen. We need to determine the focal length of the lens.
Step 2: Convert units
Convert the dimensions of the slide and the screen from meters to millimeters for consistency:
- Slide dimensions: 35 mm x 23 mm
- Screen dimensions: 2 m x 2 m = 2000 mm x 2000 mm
Step 3: Calculate magnification
The magnification (M) is given by the formula:
M=VU
Where:
- V = image distance (distance from the lens to the screen)
- U = object distance (distance from the lens to the slide)
For the width of the slide:
- U=35 mm
- V=2000 mm
Calculating magnification for the width:
M=200035≈57.14
For the height of the slide:
- U=23 mm
- V=2000 mm
Calculating magnification for the height:
M=200023≈86.96
Step 4: Choose the minimum magnification
Since we want to project the slide as a square, we will consider the minimum magnification, which is approximately 57.14.
Step 5: Relate object distance to image distance
Using the magnification formula:
M=VU
We can rearrange it to find U:
U=VM
Substituting V=10 m (which is 10000 mm) and M≈57.14:
U=1000057.14≈175.0 mm
Step 6: Apply the lens formula
The lens formula is given by:
1f=1V−1U
Substituting V=10000 mm and U=−175.0 mm (the object distance is taken as negative):
1f=110000−1−175
1f=110000+1175
Step 7: Calculate the focal length
Finding a common denominator and calculating:
1f=110000+1175
Calculating 1175 in terms of 10000:
1175=10000175×10000≈57.1410000
So:
1f=1+57.1410000=58.1410000
Thus:
f≈1000058.14≈172.0 mm
Step 8: Convert to centimeters
Converting to centimeters:
f≈17.2 cm
Final Answer
The focal length of the lens in the projector should be approximately 17.2 cm.
We need to project a 35 mm x 23 mm slide onto a 2 m x 2 m screen, with the lens positioned 10 m away from the screen. We need to determine the focal length of the lens.
Convert the dimensions of the slide and the screen from meters to millimeters for consistency:
- Slide dimensions: 35 mm x 23 mm
- Screen dimensions: 2 m x 2 m = 2000 mm x 2000 mm
The magnification (M) is given by the formula:
M=VU
Where:
- V = image distance (distance from the lens to the screen)
- U = object distance (distance from the lens to the slide)
- U=35 mm
- V=2000 mm
M=200035≈57.14
- U=23 mm
- V=2000 mm
M=200023≈86.96
Since we want to project the slide as a square, we will consider the minimum magnification, which is approximately 57.14.
Using the magnification formula:
M=VU
We can rearrange it to find U:
U=VM
Substituting V=10 m (which is 10000 mm) and M≈57.14:
U=1000057.14≈175.0 mm
The lens formula is given by:
1f=1V−1U
Substituting V=10000 mm and U=−175.0 mm (the object distance is taken as negative):
1f=110000−1−175
1f=110000+1175
Finding a common denominator and calculating:
1f=110000+1175
Calculating 1175 in terms of 10000:
1175=10000175×10000≈57.1410000
So:
1f=1+57.1410000=58.1410000
Thus:
f≈1000058.14≈172.0 mm
Converting to centimeters:
f≈17.2 cm
The focal length of the lens in the projector should be approximately 17.2 cm.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
A biconvex lens is used to project a slide on screen. The slide is 2cm high and placed at 10cm from the lens. The image is 18cm high. What is the focal length of the lens?
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View Solution
Knowledge Check
- Question 1 - Select One
An object is placed at a distance of 1.5m from a screen and a convex lens is interposed between them. The magnification produced is 4. What is the focal length of the lens ?
A1mB0.5mC0.24mD2m
Find the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cmView SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cmView SolutionA point object is kept at a distance of 2 m from a parabolic reflecting surface y2=2x . An equiconvex lens is kept at a distance of 1.80 m from the parabolic surface. The focal length of the lens is 20 cm . Find the position from origin of the image in cm, after reflection from the surface.
_S01_032_Q01.png) View Solution
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placedon the optic axis of lens at a distnace between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
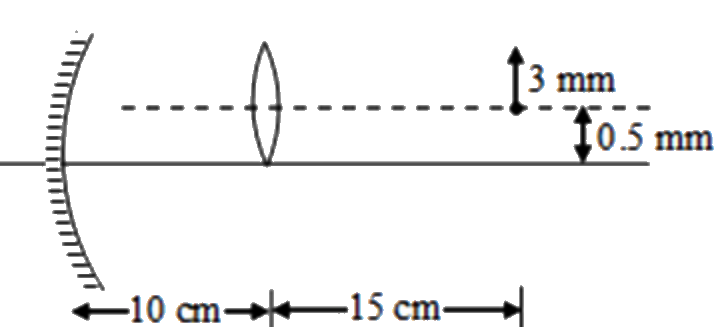 View Solution
View SolutionFind the power of a concave lens of focal length 2m.
View SolutionThe filament of lamp is 80 cm from a screen and a converging lens forms an image of it on a screen, magnified three times. Find the distance of the lens from the filament and the focal length of the lens.
View SolutionA convex lens of focal length 15cm is split into two halves and the two halves are placed at a separation of 120cm. Between, the two halves of convex lens a plane mirror is placed horizontal and at a distance of 4mm below the principal axis of the lens halves. An object of length 2mm is placed at a distance of 20cm from one half lens as shown in figure.

Find the position and size of the final image.
Trace the path of rays forming the image.View Solution

